Lets c.........if a right triangle..............has two sides of 8 and 7..........how long is the hypotenuse?.......

The Pythagorean Theorem

Learning Objective(s)

·         Use the Pythagorean Theorem to find the unknown side of a right triangle.

·         Solve application problems involving the Pythagorean Theorem.

Introduction

A long time ago, a Greek mathematician named Pythagoras discovered an interesting property about right triangles: the sum of the squares of the lengths of each of the triangle’s legs is the same as the square of the length of the triangle’s hypotenuse. This property—which has many applications in science, art, engineering, and architecture—is now called the Pythagorean Theorem.

Let’s take a look at how this theorem can help you learn more about the construction of triangles. And the best part—you don’t even have to speak Greek to apply Pythagoras’ discovery.

The Pythagorean Theorem

Pythagoras studied right triangles, and the relationships between the legs and the hypotenuse of a right triangle, before deriving his theory.

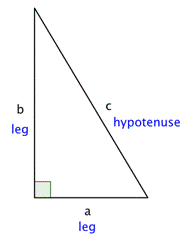
The Pythagorean Theorem

If a and b are the lengths of the legs of a right triangle and c is the length of the hypotenuse, then the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse. This relationship is represented by the formula:

In the box above, you may have noticed the word “square,” as well as the small 2s to the top right of the letters in 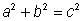. To square a number means to multiply it by itself. So, for example, to square the number 5 you multiply 5 • 5, and to square the number 12, you multiply 12 • 12. Some common squares are shown in the table below.

Number	Number Times Itself	Square
1	12 = 1 • 1	1
2	22 = 2 • 2	4
3	32 = 3 • 3	9
4	42 = 4 • 4	16
5	52 = 5 • 5	25
10	102 = 10 • 10	100

When you see the equation 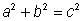, you can think of this as “the length of side a times itself, plus the length of side b times itself is the same as the length of side c times itself.”

Let’s try out all of the Pythagorean Theorem with an actual right triangle.

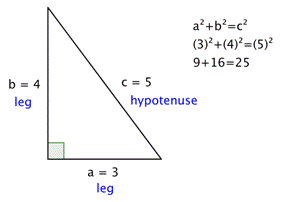
This theorem holds true for this right triangle—the sum of the squares of the lengths of both legs is the same as the square of the length of the hypotenuse. And, in fact, it holds true for all right triangles.

The Pythagorean Theorem can also be represented in terms of area. In any right triangle, the area of the square drawn from the hypotenuse is equal to the sum of the areas of the squares that are drawn from the two legs. You can see this illustrated below in the same 3-4-5 right triangle.

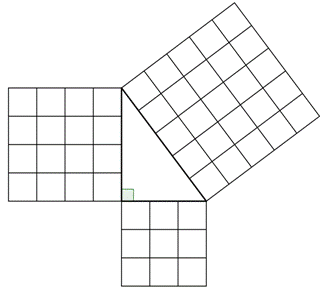
Note that the Pythagorean Theorem only works with right triangles.

Finding the Length of the Hypotenuse

You can use the Pythagorean Theorem to find the length of the hypotenuse of a right triangle if you know the length of the triangle’s other two sides, called the legs. Put another way, if you know the lengths of a and b, you can find c.

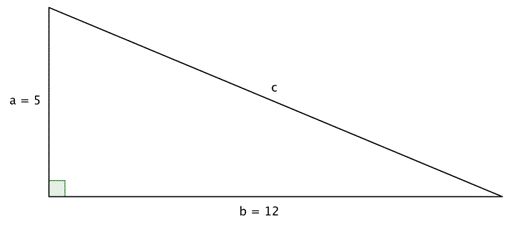
In the triangle above, you are given measures for legs a and b: 5 and 12, respectively. You can use the Pythagorean Theorem to find a value for the length of c, the hypotenuse.

	The Pythagorean Theorem.
	Substitute known values for a andb.
	Evaluate.
	Simplify. To find the value of c, think about a number that, when multiplied by itself, equals 169. Does 10 work? How about 11? 12? 13? (You can use a calculator to multiply if the numbers are unfamiliar.)
13 = c	The square root of 169 is 13.