TRIANGLE PROPORTIONALITY THEOREM

Similar triangles can be located any number of places, including one inside the other. And if you're working with a big problem, there may be a third similar triangle inside of the first two. And technically there could be a fourth one, even smaller, inside of the third.
But before Leonardo DiCaprio or Joseph Gordon-Levitt show up and draw us into a ridiculous triangle-ception situation, let's just state for the record that we're only going to deal with the first two, which are actually created by taking one triangle and shooting a line through it. Because if that line is parallel to one side of the triangle, it'll create two similar triangles.
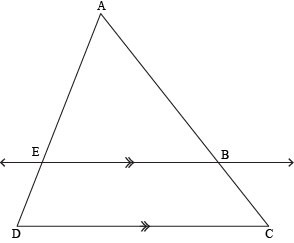
Here, ∆ACD ~ ∆ABE. We'll prove this a little later. For now, we're going to focus on the chopped-up side pieces.
In this illustration, line EB is parallel to side DC. We can see that it intersects sides AC and AD. This creates proportional segments:
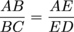
In fact, we even have a theorem about this: the Triangle Proportionality Theorem. Apparently, mathematicians got quite a giggle when they first came up with it, since it's earned the nickname "The Side-Splitter Theorem." To be honest, we don't really get it. It must be an inside joke.
The Triangle Proportionality Theorem says that if a line is parallel to one side of a triangle, then it splits the other two sides into proportional sections.
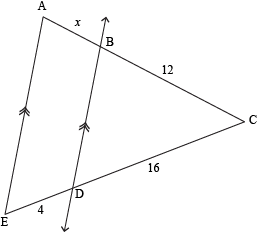
We can use this theorem to find the value of x in ∆ACE. We're given that line BD is parallel to side AE, and three of the resulting segment lengths are also given. To find the missing piece, set up a proportion comparing the side lengths:
16⁄4 = 12⁄x
No comments:
Post a Comment