Why?  Well the book ......Music of the primes......ghost written by my father................said that the harmonic series itself held the key..........and the Euler didn't see other stuff with it......a big hint.....of course he throws out false info......like the military would do .......counter intel...........but the series itself has other interesting features..........u just don't think that those things are connected in the ways they are....

Comparison test[edit]

One way to prove divergence is to compare the harmonic series with another divergent series, where each denominator is replaced with the next-largest power of two:

${\displaystyle {\begin{aligned}&1\;\;+\;\;{\frac {1}{2}}\;\;+\;\;{\frac {1}{3}}\,+\,{\frac {1}{4}}\;\;+\;\;{\frac {1}{5}}\,+\,{\frac {1}{6}}\,+\,{\frac {1}{7}}\,+\,{\frac {1}{8}}\;\;+\;\;{\frac {1}{9}}\,+\,\cdots \\[12pt]>\;\;\;&1\;\;+\;\;{\frac {1}{2}}\;\;+\;\;{\frac {1}{4}}\,+\,{\frac {1}{4}}\;\;+\;\;{\frac {1}{8}}\,+\,{\frac {1}{8}}\,+\,{\frac {1}{8}}\,+\,{\frac {1}{8}}\;\;+\;\;{\frac {1}{16}}\,+\,\cdots \end{aligned}}}$

Each term of the harmonic series is greater than or equal to the corresponding term of the second series, and therefore the sum of the harmonic series must be greater than the sum of the second series. However, the sum of the second series is infinite:

${\displaystyle {\begin{aligned}&1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}+{\frac {1}{4}}\right)+\left({\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}\right)+\left({\frac {1}{16}}+\cdots +{\frac {1}{16}}\right)+\cdots \\[12pt]=\;\;&1\;\;+\;\;{\frac {1}{2}}\;\;+\;\;{\frac {1}{2}}\;\;+\;\;{\frac {1}{2}}\;\;+\;\;{\frac {1}{2}}\;\;+\;\;\cdots \;\;=\;\;\infty \end{aligned}}}$

It follows (by the comparison test) that the sum of the harmonic series must be infinite as well. More precisely, the comparison above proves that

${\displaystyle \sum _{n=1}^{2^{k}}\,{\frac {1}{n}}\;\geq \;1+{\frac {k}{2}}}$

for every positive integer k.

This proof, proposed by Nicole Oresme in around 1350, is considered by many in the mathematical community to be a high point of medieval mathematics. It is still a standard proof taught in mathematics classes today. Cauchy's condensation test is a generalization of this argument.

Integral test[edit]

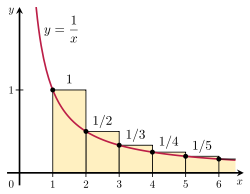
It is possible to prove that the harmonic series diverges by comparing its sum with an improper integral. Specifically, consider the arrangement of rectangles shown in the figure to the right. Each rectangle is 1 unit wide and 1/n units high, so the total area of the infinite number of rectangles is the sum of the harmonic series:

${\displaystyle {\begin{array}{c}{\text{area of}}\\{\text{rectangles}}\end{array}}=1\,+\,{\frac {1}{2}}\,+\,{\frac {1}{3}}\,+\,{\frac {1}{4}}\,+\,{\frac {1}{5}}\,+\,\cdots }$

However, the total area under the curve y = 1/x from 1 to infinity is given by an improper integral:

${\displaystyle {\begin{array}{c}{\text{area under}}\\{\text{curve}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}\,dx\;=\;\ln \infty \;=\;\infty .}$