An Interactive Guide To The Fourier Transform
The Fourier Transform is one of deepest insights ever made. Unfortunately, the meaning is buried within dense equations:
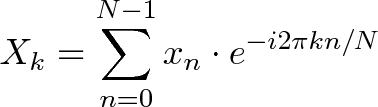
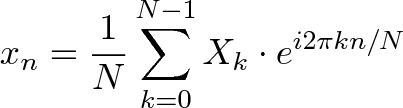
Yikes. Rather than jumping into the symbols, let's experience the key idea firsthand. Here's a plain-English metaphor:
If all goes well, we'll have an aha! moment and intuitively realize why the Fourier Transform is possible. We'll save the detailed math analysis for the follow-up.
This isn't a force-march through the equations, it's the casual stroll I wish I had. Onward!
The Fourier Transform changes our perspective from consumer to producer, turning What do I have? into How was it made?
In other words: given a smoothie, let's find the recipe.
Why? Well, recipes are great descriptions of drinks. You wouldn't share a drop-by-drop analysis, you'd say "I had an orange/banana smoothie". A recipe is more easily categorized, compared, and modified than the object itself.
So... given a smoothie, how do we find the recipe?
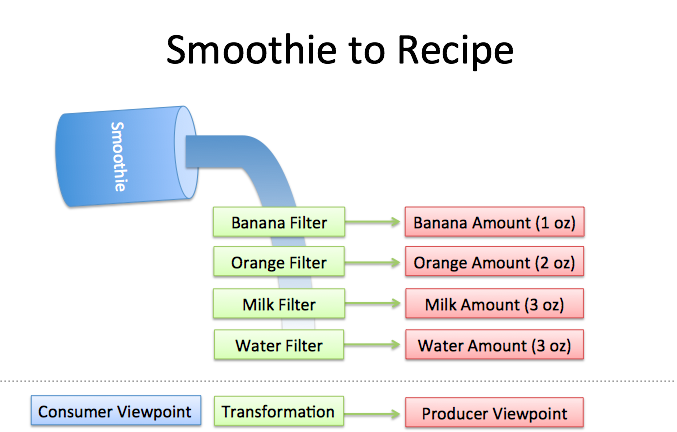
Well, imagine you had a few filters lying around:
Whoa. This concept is mind-blowing, and poor Joseph Fourier had his idea rejected at first. (Really Joe, even a staircase pattern can be made from circles?)
And despite decades of debate in the math community, we expect students to internalize the idea without issue. Ugh. Let's walk through the intuition.
The Fourier Transform finds the recipe for a signal, like our smoothie process:
The Fourier Transform is about circular paths (not 1-d sinusoids) and Euler's formula is a clever way to generate one:

Must we use imaginary exponents to move in a circle? Nope. But it's convenient and compact. And sure, we can describe our path as coordinated motion in two dimensions (real and imaginary), but don't forget the big picture: we're just moving in a circle.
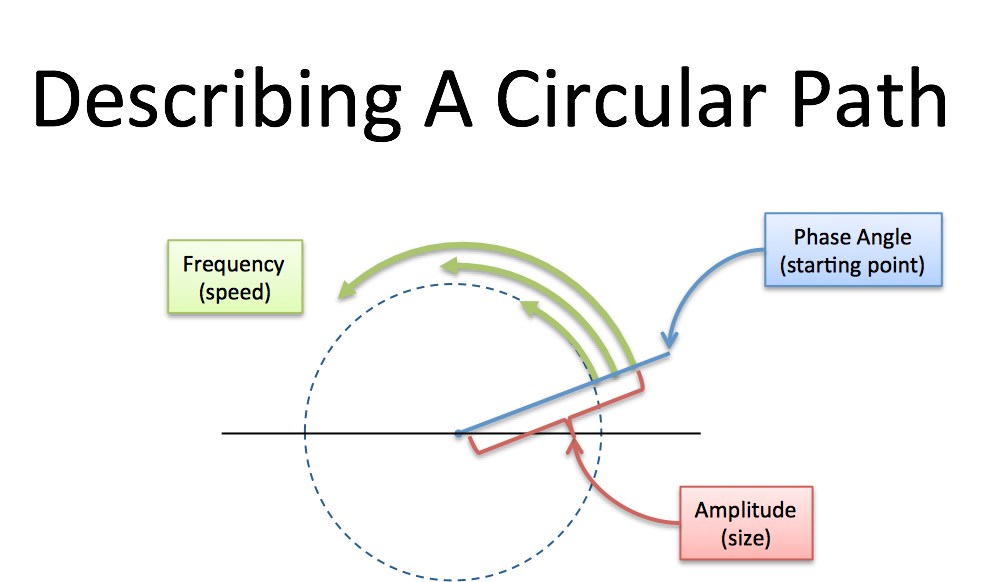
Every circular path needs a size, speed, and starting angle (amplitude/frequency/phase). We can even combine paths: imagine tiny motorcars, driving in circles at different speeds.
The combined position of all the cycles is our signal, just like the combined flavor of all the ingredients is our smoothie.
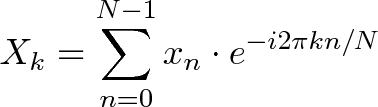
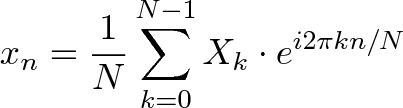
Yikes. Rather than jumping into the symbols, let's experience the key idea firsthand. Here's a plain-English metaphor:
- What does the Fourier Transform do? Given a smoothie, it finds the recipe.
- How? Run the smoothie through filters to extract each ingredient.
- Why? Recipes are easier to analyze, compare, and modify than the smoothie itself.
- How do we get the smoothie back? Blend the ingredients.
- The Fourier Transform takes a time-based pattern, measures every possible cycle, and returns the overall "cycle recipe" (the amplitude, offset, & rotation speed for every cycle that was found).
If all goes well, we'll have an aha! moment and intuitively realize why the Fourier Transform is possible. We'll save the detailed math analysis for the follow-up.
This isn't a force-march through the equations, it's the casual stroll I wish I had. Onward!
From Smoothie to Recipe
A math transformation is a change of perspective. We change our notion of quantity from "single items" (lines in the sand, tally system) to "groups of 10" (decimal) depending on what we're counting. Scoring a game? Tally it up. Multiplying? Decimals, please.The Fourier Transform changes our perspective from consumer to producer, turning What do I have? into How was it made?
In other words: given a smoothie, let's find the recipe.
Why? Well, recipes are great descriptions of drinks. You wouldn't share a drop-by-drop analysis, you'd say "I had an orange/banana smoothie". A recipe is more easily categorized, compared, and modified than the object itself.
So... given a smoothie, how do we find the recipe?

Well, imagine you had a few filters lying around:
- Pour through the "banana" filter. 1 oz of bananas are extracted.
- Pour through the "orange" filter. 2 oz of oranges.
- Pour through the "milk" filter. 3 oz of milk.
- Pour through the "water" filter. 3 oz of water.
- Filters must be independent. The banana filter needs to capture bananas, and nothing else. Adding more oranges should never affect the banana reading.
- Filters must be complete. We won't get the real recipe if we leave out a filter ("There were mangoes too!"). Our collection of filters must catch every possible ingredient.
- Ingredients must be combine-able. Smoothies can be separated and re-combined without issue (A cookie? Not so much. Who wants crumbs?). The ingredients, when separated and combined in any order, must make the same result.
See The World As Cycles
The Fourier Transform takes a specific viewpoint: What if any signal could be filtered into a bunch of circular paths?Whoa. This concept is mind-blowing, and poor Joseph Fourier had his idea rejected at first. (Really Joe, even a staircase pattern can be made from circles?)
And despite decades of debate in the math community, we expect students to internalize the idea without issue. Ugh. Let's walk through the intuition.
The Fourier Transform finds the recipe for a signal, like our smoothie process:
- Start with a time-based signal
- Apply filters to measure each possible "circular ingredient"
- Collect the full recipe, listing the amount of each "circular ingredient"
- If earthquake vibrations can be separated into "ingredients" (vibrations of different speeds & amplitudes), buildings can be designed to avoid interacting with the strongest ones.
- If sound waves can be separated into ingredients (bass and treble frequencies), we can boost the parts we care about, and hide the ones we don't. The crackle of random noise can be removed. Maybe similar "sound recipes" can be compared (music recognition services compare recipes, not the raw audio clips).
- If computer data can be represented with oscillating patterns, perhaps the least-important ones can be ignored. This "lossy compression" can drastically shrink file sizes (and why JPEG and MP3 files are much smaller than raw .bmp or .wav files).
- If a radio wave is our signal, we can use filters to listen to a particular channel. In the smoothie world, imagine each person paid attention to a different ingredient: Adam looks for apples, Bob looks for bananas, and Charlie gets cauliflower (sorry bud).
Think With Circles, Not Just Sinusoids
One of my giant confusions was separating the definitions of "sinusoid" and "circle".- A "sinusoid" is a specific back-and-forth pattern (a sine or cosine wave), and 99% of the time, it refers to motion in one dimension.
- A "circle" is a round, 2d pattern you probably know. If you enjoy using 10-dollar words to describe 10-cent ideas, you might call a circular path a "complex sinusoid".
The Fourier Transform is about circular paths (not 1-d sinusoids) and Euler's formula is a clever way to generate one:

Must we use imaginary exponents to move in a circle? Nope. But it's convenient and compact. And sure, we can describe our path as coordinated motion in two dimensions (real and imaginary), but don't forget the big picture: we're just moving in a circle.
Following Circular Paths
Let's say we're chatting on the phone and, like usual, I want us to draw the same circle simultaneously. (You promised!) What should I say?- How big is the circle? (Amplitude, i.e. size of radius)
- How fast do we draw it? (Frequency. 1 circle/second is a frequency of 1 Hertz (Hz) or 2*pi radians/sec)
- Where do we start? (Phase angle, where 0 degrees is the x-axis)

Every circular path needs a size, speed, and starting angle (amplitude/frequency/phase). We can even combine paths: imagine tiny motorcars, driving in circles at different speeds.
The combined position of all the cycles is our signal, just like the combined flavor of all the ingredients is our smoothie.
No comments:
Post a Comment