Like that.....but half as small........the below has hyp of 2...........mine i formed....has hyp of 1......side of 1/2.....therefore half of the square root of 3........double that and it is the square root of 3......the length of the major axis of the ellipse formed by two interlocking unit circles......centered along the X axis.......at 1/2 and - 1/2.........

4

THE 30°-60°-90° TRIANGLE

THERE ARE TWO special triangles in trigonometry. One is the 30°-60°-90° triangle. The other is the isosceles right triangle. They are special because, with simple geometry, we can know the ratios of their sides. 

Theorem.  In a 30°-60°-90° triangle the sides are in the ratio 1 : 2 : .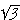

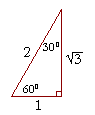
We will prove that below.

(For the definition of measuring angles by "degrees," see Topic 12.)

Note that the smallest side, 1, is opposite the smallest angle, 30°; while the largest side, 2, is opposite the largest angle, 90°.  (Theorem 6). (For, 2 is larger than 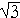.  Also, while 1 : 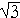: 2 correctly corresponds to the sides opposite 30°-60°-90°, many find the sequence 1 : 2 :  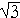easier to remember.)

The cited theorems are from the Appendix, Some theorems of plane geometry.

Here are examples of how we take advantage of knowing those ratios.  First, we can evaluate the functions of 60° and 30°.

Example 1.   Evaluate cos 60°.

Answer.  For any problem involving a 30°-60°-90° triangle, the student should not use a table.  The student should sketch the triangle and place the ratio numbers.

Since the cosine is the ratio of the adjacent side to the hypotenuse, you can see that cos 60° = ½.