2 - 11................ten numbers...........two fives.....................5 primes............5 non primes.................the primes sum to 28............the non primes sum to 37.........adding single digits to the double digits of either...................gives u ten.........2 + 8 = 10..............3 + 7 = 10..............10 * 10 = 100.......whose sum is 5050...............from 1 - 100.......................................4 primes in single digits........1 in double digits................like 14i.........but reversed........with an imagination........u can flip the number.........or 41........................the 13th prime..........................said together........a garbled pi............the same with the non primes......symmetry........................4 in single digits, 1 in double digits.............a 10 of all numbers.........................


The plots above show the real and imaginary parts of plotted in the complex plane together with the complex modulus of . As can be seen, in right half-plane, the function is fairly flat, but with a large number of horizontal ridges. It is precisely along these ridges that the nontrivial zeros of lie.
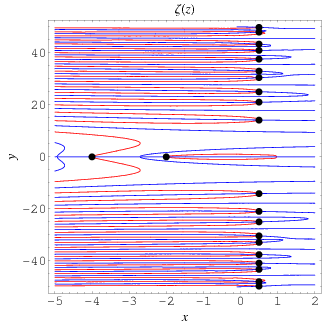
The position of the complex zeros can be seen slightly more easily by plotting the contours of zero real (red) and imaginary (blue) parts, as illustrated above. The zeros (indicated as black dots) occur where the curves intersect.