Unit Circle

The "Unit Circle" is a circle with a radius of 1.
Being so simple, it is a great way to learn and talk about lengths and angles.The center is put on a graph where the x axis and y axis cross, so we get this neat arrangement here.

Sine, Cosine and Tangent
Because the radius is 1, we can directly measure sine, cosine and tangent.
cos 0° = 1, sin 0° = 0 and tan 0° = 0

cos 90° = 0, sin 90° = 1 and tan 90° is undefined
Try It Yourself!
Have a try! Move the mouse around to see how different angles (in radians or degrees) affect sine, cosine and tangentThe "sides" can be positive or negative according to the rules of Cartesian coordinates. This makes the sine, cosine and tangent change between positive and negative values also.
Also try the Interactive Unit Circle.

Pythagoras
Pythagoras' Theorem says that for a right angled triangle, the square of the long side equals the sum of the squares of the other two sides:
x2 + y2 = 12
But 12 is just 1, so:
x2 + y2 = 1
(the equation of the unit circle)
Also, since x=cos and y=sin, we get:(the equation of the unit circle)
(cos(θ))2 + (sin(θ))2 = 1
a useful "identity"
Important Angles: 30°, 45° and 60°
You should try to remember sin, cos and tan for the angles 30°, 45° and 60°.Yes, yes, it is a pain to have to remember things, but it will make life easier when you know them, not just in exams, but other times when you need to do quick estimates, etc.
These are the values you should remember!
| Angle | Sin | Cos | Tan=Sin/Cos |
|---|---|---|---|
| 30° | 1 √3 = √3 3 | ||
| 45° | 1 | ||
| 60° | √3 |
How To Remember?
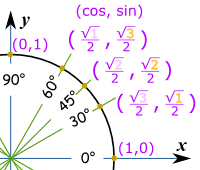
sin(30°) = √12 = 12 (because √1 = 1)
sin(45°) = √22
sin(60°) = √32
And cos goes "3,2,1"
cos(30°) = √32
cos(45°) = √22
cos(60°) = √12 = 12
Just 3 Numbers
In fact, knowing 3 numbers is enough: 12 , √22 and √32Because they work for both cos and sin:
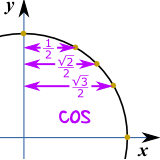 | 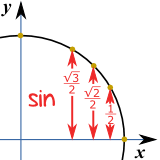 |
What about tan?
Well, tan = sin/cos, so we can calculate it like this:
tan(30°) =sin(30°)cos(30°) = 1/2√3/2 = 1√3 = √33 *
tan(45°) =sin(45°)cos(45°) = √2/2√2/2 = 1
tan(60°) =sin(60°)cos(60°) = √3/21/2 = √3
* Note: writing 1√3 may cost you marks (see Rational Denominators), so instead use √33Quick Sketch
Another way to help you remember 30° and 60° is to make a quick sketch:| Draw a triangle with side lengths of 2 | 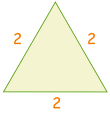 | |
| Cut in half. Pythagoras says the new side is √3
12 + (√3)2 = 22
1 + 3 = 4
| 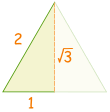 | |
| Then use sohcahtoa for sin, cos or tan | 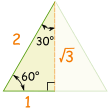 |
No comments:
Post a Comment