Background[edit]
Notation[edit]
While there are several notational conventions for representing repeating decimals, none of them are accepted universally. In the United States, the convention is generally to indicate a repeating decimal by drawing a horizontal line (a vinculum) above the repetend ( ). In mainland China, the convention is to place dots above the outermost numerals of the repetend (
). In mainland China, the convention is to place dots above the outermost numerals of the repetend ( ). Another notation sometimes employed in Europe is to enclose the repetend in parentheses (
). Another notation sometimes employed in Europe is to enclose the repetend in parentheses ( ). Repeating decimals may also be represented by three periods (an ellipsis, e.g., 0.333…), although this method introduces uncertainty as to which digits should be repeated or even whether repetition is occurring at all, since such ellipses are also employed for irrational decimals such as 3.14159…
). Repeating decimals may also be represented by three periods (an ellipsis, e.g., 0.333…), although this method introduces uncertainty as to which digits should be repeated or even whether repetition is occurring at all, since such ellipses are also employed for irrational decimals such as 3.14159…
 ). In mainland China, the convention is to place dots above the outermost numerals of the repetend (
). In mainland China, the convention is to place dots above the outermost numerals of the repetend ( ). Another notation sometimes employed in Europe is to enclose the repetend in parentheses (
). Another notation sometimes employed in Europe is to enclose the repetend in parentheses ( ). Repeating decimals may also be represented by three periods (an ellipsis, e.g., 0.333…), although this method introduces uncertainty as to which digits should be repeated or even whether repetition is occurring at all, since such ellipses are also employed for irrational decimals such as 3.14159…
). Repeating decimals may also be represented by three periods (an ellipsis, e.g., 0.333…), although this method introduces uncertainty as to which digits should be repeated or even whether repetition is occurring at all, since such ellipses are also employed for irrational decimals such as 3.14159…| Fraction | Ellipsis | Vinculum | Dots | Parentheses |
|---|---|---|---|---|
| 1/9 | 0.111… | 0.1 |  | 0.(1) |
| 1/3 | 0.333… | 0.3 |  | 0.(3) |
| 2/3 | 0.666… | 0.6 | 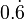 | 0.(6) |
| 9/11 | 0.8181… | 0.81 |  | 0.(81) |
| 7/12 | 0.58333… | 0.583 |  | 0.58(3) |
| 1/81 | 0.012345679… | 0.012345679 |  | 0.(012345679) |
| 22/7 | 3.142857142857… | 3.142857 |  | 3.(142857) |
In English, there are various ways to read repeating decimals aloud. Some common ones (for ⅓) include "zero point three repeating", "zero point three repeated", "zero point three recurring", and "zero point three into infinity". Mention of the initial zero may also be omitted.
Decimal expansion and recurrence sequence[edit]
In order to convert a rational number represented as a fraction into decimal form, one may use long division. For example, consider the rational number 5/74:
. .
0.0675
74 ) 5.00000
4.44
560
518
420
370
500
etc. Observe that at each step we have a remainder; the successive remainders displayed above are 56, 42, 50. When we arrive at 50 as the remainder, and bring down the "0", we find ourselves dividing 500 by 74, which is the same problem we began with. Therefore the decimal repeats: 0.0675 675 675 ….
Every rational number is either a terminating or repeating decimal[edit]
For any given divisor, only finitely many different remainders can occur. In the example above, the 74 possible remainders are 0, 1, 2, …, 73. If at any point in the division the remainder is 0, the expansion terminates at that point. If 0 never occurs as a remainder, then the division process continues forever, and eventually a remainder must occur that has occurred before. The next step in the division will yield the same new digit in the quotient, and the same new remainder, as the previous time the remainder was the same. Therefore the following division will repeat the same results.
Every repeating or terminating decimal is a rational number[edit]
Each repeating decimal number satisfies a linear equation with integer coefficients, and its unique solution is a rational number. To illustrate the latter point, the number α = 5.8144144144… above satisfies the equation 10000α − 10α = 58144.144144… − 58.144144… = 58086, whose solution is α = 58086/9990 = 3227/555. The process of how to find these integer coefficients is described below.
Fractions with prime denominators[edit]
A fraction in lowest terms with a prime denominator other than 2 or 5 (i.e. coprime to 10) always produces a repeating decimal. The length of the repetend (period of the repeating decimal) of 1/p is equal to the order of 10 modulo p. If 10 is a primitive root modulo p, the repetend length is equal to p − 1; if not, the repetend length is a factor of p − 1. This result can be deduced from Fermat's little theorem, which states that 10p−1 = 1 (mod p).
The base-10 repetend of the reciprocal of any prime number greater than 5 is divisible by 9.[3]
If the repetend length of 1/p for prime p is equal to p − 1 then the repetend, expressed as an integer, is called a cyclic number.
The period length of 1/n are
- 0, 0, 1, 0, 0, 1, 6, 0, 1, 0, 2, 1, 6, 6, 1, 0, 16, 1, 18, 0, 6, 2, 22, 1, 0, 6, 3, 6, 28, 1, 15, 0, 2, 16, 6, 1, 3, 18, 6, 0, 5, 6, 21, 2, 1, 22, 46, 1, 42, 0, 16, 6, 13, 3, 2, 6, 18, 28, 58, 1, 60, 15, 6, 0, 6, 2, 33, 16, 22, 6, 35, 1, 8, 3, 1, ... (sequence A051626 in OEIS)
The periodic part of 1/n are
- 0, 0, 3, 0, 0, 6, 142857, 0, 1, 0, 09, 3, 076923, 714285, 6, 0, 0588235294117647, 5, 052631578947368421, 0, 047619, 45, 0434782608695652173913, 6, 0, 384615, 037, 571428, 0344827586206896551724137931, 3, ... (sequence A036275 in OEIS)
The period length of 1/(nth prime) are
- 0, 1, 0, 6, 2, 6, 16, 18, 22, 28, 15, 3, 5, 21, 46, 13, 58, 60, 33, 35, 8, 13, 41, 44, 96, 4, 34, 53, 108, 112, 42, 130, 8, 46, 148, 75, 78, 81, 166, 43, 178, 180, 95, 192, 98, 99, 30, 222, 113, 228, 232, 7, 30, 50, 256, 262, 268, 5, 69, 28, ... (sequence A002371 in OEIS)
The least prime p which 1/p with period length n are
- 3, 11, 37, 101, 41, 7, 239, 73, 333667, 9091, 21649, 9901, 53, 909091, 31, 17, 2071723, 19, 1111111111111111111, 3541, 43, 23, 11111111111111111111111, 99990001, 21401, 859, 757, 29, 3191, 211, ... (sequence A007138 in OEIS)
The least prime p which k/p has n different cycles (1≤k≤p-1) are
- 7, 3, 103, 53, 11, 79, 211, 41, 73, 281, 353, 37, 2393, 449, 3061, 1889, 137, 2467, 16189, 641, 3109, 4973, 11087, 1321, 101, 7151, 7669, 757, 38629, 1231, ... (sequence A054471 in OEIS)
Cyclic numbers[edit]
Main article: Cyclic number
Examples of fractions belonging to this group are:
- 1/7 = 0.142857 ; 6 repeating digits
- 1/17 = 0.05882352 94117647 ; 16 repeating digits
- 1/19 = 0.052631578 947368421 ; 18 repeating digits
- 1/23 = 0.04347826086 95652173913 ; 22 repeating digits
- 1/29 = 0.0344827 5862068 9655172 4137931 ; 28 repeating digits
- 1/97 = 0.01030927 83505154 63917525 77319587 62886597 93814432 98969072 16494845 36082474 22680412 37113402 06185567 ; 96 repeating digits
The list can go on to include the fractions 1/47, 1/59, 1/61, 1/109, 1/131, 1/149, etc. (sequence A001913 in OEIS)
Every proper multiple of a cyclic number (that is, a multiple having the same number of digits) is a rotation.
- 1/7 = 1 × 0.142857… = 0.142857…
- 3/7 = 3 × 0.142857… = 0.428571…
- 2/7 = 2 × 0.142857… = 0.285714…
- 6/7 = 6 × 0.142857… = 0.857142…
- 4/7 = 4 × 0.142857… = 0.571428…
- 5/7 = 5 × 0.142857… = 0.714285…
The reason for the cyclic behavior is apparent from an arithmetic exercise of long division of 1⁄7: the sequential remainders are the cyclic sequence {1, 3, 2, 6, 4, 5}. See also the article 142857 for more properties of this cyclic number.
A proper prime is a prime p which ends in the digit 1 in base 10 and whose reciprocal in base 10 has a repetend with length p-1. In such primes, each digit 0, 1, ..., 9 appears in the repeating sequence the same number of times as does each other digit (namely, (p-1)/10 times). The smallest proper prime is 61.[4]:166 (sequence A073761in OEIS)
Other reciprocals of primes[edit]
Some reciprocals of primes that do not generate cyclic numbers are:
- 1/3 = 0.333… which has a period of 1.
- 1/11 = 0.090909… which has a period of 2.
- 1/13 = 0.076923… which has a period of 6.
- 1/37 = 0.027… which has a period of 3.
- 1/41 = 0.02439… which has a period of 5.
The reason is that 3 is a divisor of 9, 11 is a divisor of 99, 41 is a divisor of 99999, etc. To find the period of 1/p, we can check whether the prime p divides some number 99…9 in which the number of digits divides p - 1. Since the period is never greater than p - 1, we can obtain this by calculating 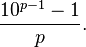 For example, for 11 we get
For example, for 11 we get
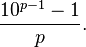 For example, for 11 we get
For example, for 11 we get
No comments:
Post a Comment