Break it on down......
Reading from the table for figures close to A:
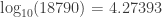 and
and 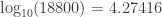
Now if we linearly interpolate between these two figures, for greater accuracy, we obtain the approximation
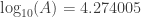
Reading from the table for figures close to B:
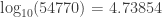 and
and 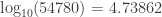
Now if we linearly interpolate between these two figures, for greater accuracy, we obtain the approximation
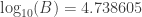
Next, we use the property of logarithms mentioned earlier to estimate the logarithm of AB:
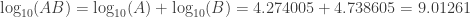
The process of adding logarithms is very easy, and this is the point of the method. We’ve taken a relatively complicated problem (multiplying two numbers that have many digits) and converted it to a much easier problem (adding two numbers that have many digits). Now we have to convert the result back into the realm of the initial problem.
Reading from the table for figures close to A:
Now if we linearly interpolate between these two figures, for greater accuracy, we obtain the approximation
Reading from the table for figures close to B:
Now if we linearly interpolate between these two figures, for greater accuracy, we obtain the approximation
Next, we use the property of logarithms mentioned earlier to estimate the logarithm of AB:
The process of adding logarithms is very easy, and this is the point of the method. We’ve taken a relatively complicated problem (multiplying two numbers that have many digits) and converted it to a much easier problem (adding two numbers that have many digits). Now we have to convert the result back into the realm of the initial problem.
Comments
Post a Comment