The figures above highlight the zeros in the complex plane by plotting
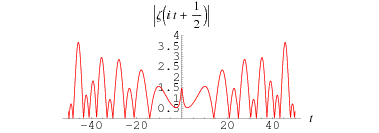 The above plot shows The above plot shows
|
Friday, February 16, 2018
Two lines.......he found in 4 d..................perpendicular to each other.......at a 90 angle.......................zeros......................
Subscribe to:
Post Comments (Atom)
No comments:
Post a Comment