Riemann Zeta Function Zeros

Zeros of the
Riemann zeta function 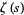
come in two different types. So-called "trivial zeros" occur at
all negative even integers
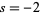
,
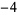
,
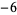
, ..., and "nontrivial zeros" occur at certain values of
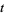
satisfying
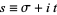 |
(1)
|
for
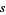
in the "
critical strip"
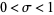
. In general, a nontrivial zero of
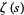
is denoted
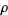
, and the
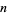
th nontrivial zero with
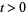
is commonly denoted
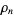
(Brent 1979; Edwards 2001, p. 43), with the corresponding value of
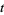
being called
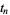
.
Wiener (1951) showed that the
prime number theorem is literally equivalent to the assertion that
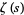
has no zeros on
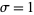
(Hardy 1999, p. 34; Havil 2003, p. 195). The
Riemann hypothesis asserts that the nontrivial zeros of
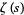
all have
real part ![sigma=R[s]=1/2](http://mathworld.wolfram.com/images/equations/RiemannZetaFunctionZeros/Inline18.gif)
, a line called the "
critical line." This is known to be true for the first
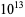
zeros.

An attractive poster plotting zeros of the
Riemann zeta function on the
critical line together with annotations for relevant historical information, illustrated above, was created by Wolfram Research (1995).
The plots above show the real and imaginary parts of
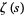
plotted in the complex plane together with the
complex modulus of
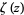
. As can be seen, in right half-plane, the function is fairly flat, but with a large number of horizontal ridges. It is precisely along these ridges that the nontrivial zeros of
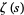
lie.
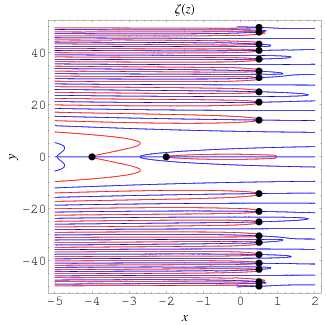
The position of the complex zeros can be seen slightly more easily by plotting the contours of zero real (red) and imaginary (blue) parts, as illustrated above. The zeros (indicated as black dots) occur where the curves intersect.
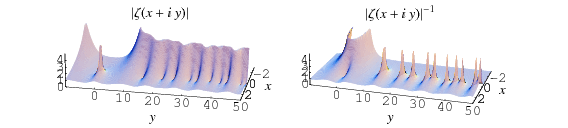
The figures above highlight the zeros in the
complex plane by plotting
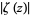
(where the zeros are dips) and
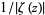
(where the zeros are peaks).
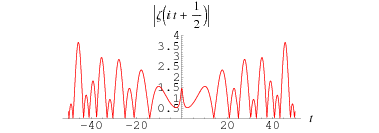
The above plot shows
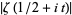
for
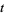
between 0 and 60. As can be seen, the first few nontrivial zeros occur at the values given in the following table (Wagon 1991, pp. 361-362 and 367-368; Havil 2003, p. 196; Odlyzko), where the corresponding negative values are also roots. The integers closest to these values are 14, 21, 25, 30, 33, 38, 41, 43, 48, 50, ... (OEIS
A002410). The numbers of nontrivial zeros less than 10,
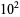
,
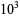
, ... are 0, 29, 649, 10142, 138069, 1747146, ... (OEIS
A072080; Odlyzko).
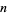 | Sloane | 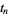 |
| 1 | A058303 | 14.134725 |
| 2 | | 21.022040 |
| 3 | | 25.010858 |
| 4 | | 30.424876 |
| 5 | | 32.935062 |
| 6 | | 37.586178 |
 An attractive poster plotting zeros of the Riemann zeta function on the critical line together with annotations for relevant historical information, illustrated above, was created by Wolfram Research (1995).
An attractive poster plotting zeros of the Riemann zeta function on the critical line together with annotations for relevant historical information, illustrated above, was created by Wolfram Research (1995).  The position of the complex zeros can be seen slightly more easily by plotting the contours of zero real (red) and imaginary (blue) parts, as illustrated above. The zeros (indicated as black dots) occur where the curves intersect.
The position of the complex zeros can be seen slightly more easily by plotting the contours of zero real (red) and imaginary (blue) parts, as illustrated above. The zeros (indicated as black dots) occur where the curves intersect.  The figures above highlight the zeros in the complex plane by plotting
The figures above highlight the zeros in the complex plane by plotting  The above plot shows
The above plot shows 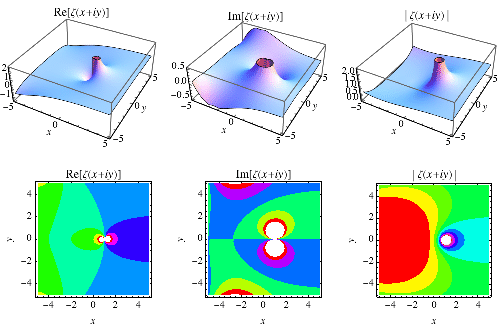
No comments:
Post a Comment