In a reg. hexagon...............all internal angles are 120..........................................so if u make diagonals.............u can form 6 triangles............with all angles whose measure are 60 degrees...........equilateral triangles.....

Hexagon

From Wikipedia, the free encyclopedia

Jump to: navigation, search

Not to be confused with Hexalgon.

For other uses, see Hexagon (disambiguation).

Regular hexagon
A regular hexagon
Type	Regular polygon
Edges and vertices	6
Schläfli symbol	{6}, t{3}
Coxeter diagram
Symmetry group	Dihedral (D6), order 2×6
Internal angle (degrees)	120°
Dual polygon	Self
Properties	Convex, cyclic, equilateral, isogonal, isotoxal

In geometry, a hexagon (from Greek ἕξ hex, "six" and γωνία, gonía, "corner, angle") is a six sided polygon or 6-gon. The total of the internal angles of any hexagon is 720°.

Contents

 [hide] 

• 1 Regular hexagon
  • 1.1 Parameters
• 2 Symmetry
• 3 Related polygons and tilings
• 4 Hexagonal structures
• 5 Tesselations by hexagons
• 6 Hexagon inscribed in a conic section
  • 6.1 Cyclic hexagon
• 7 Hexagon tangential to a conic section
• 8 Equilateral triangles on the sides of an arbitrary hexagon
• 9 Skew hexagon
  • 9.1 Petrie polygons
• 10 Convex equilateral hexagon
  • 10.1 Polyhedra with hexagons
• 11 Hexagons: natural and human-made
• 12 See also
• 13 References
• 14 External links

Regular hexagon[edit]

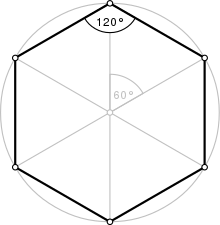
A regular hexagon has Schläfli symbol {6}^[1] and can also be constructed as a truncated equilateral triangle, t{3}, which alternates two types of edges.

A step-by-step animation of the construction of a regular hexagon using compass and straightedge, given by Euclid's Elements, Book IV, Proposition 15: this is possible as 6 ${\displaystyle =}$ 2 × 3, a product of a power of two and distinct Fermat primes.

When the side length AB is given, then you draw around the point A and around the point B a circular arc. The intersection M is the center of the circumscribed circle. Transfer the line segment AB four times on the circumscribed circle and connect the corner points.

A regular hexagon is defined as a hexagon that is both equilateral and equiangular. It is bicentric, meaning that it is both cyclic (has a circumscribed circle) and tangential (has an inscribed circle).
The common length of the sides equals the radius of the circumscribed circle, which equals ${\displaystyle {\tfrac {2{\sqrt {3}}}{3}}}$ times the apothem (radius of the inscribed circle). All internal angles are 120 degrees. A regular hexagon has 6 rotational symmetries (rotational symmetry of order six) and 6 reflection symmetries (six lines of symmetry), making up the dihedral group D₆. The longest diagonals of a regular hexagon, connecting diametrically opposite vertices, are twice the length of one side. From this it can be seen that a triangle with a vertex at the center of the regular hexagon and sharing one side with the hexagon is equilateral, and that the regular hexagon can be partitioned into six equilateral triangles.
Like squares and equilateral triangles, regular hexagons fit together without any gaps to tile the plane (three hexagons meeting at every vertex), and so are useful for constructing tessellations. The cells of a beehive honeycomb are hexagonal for this reason and because the shape makes efficient use of space and building materials. The Voronoi diagram of a regular triangular lattice is the honeycomb tessellation of hexagons. It is not usually considered a triambus, although it is equilateral.

Parameters[edit]

The maximal diameter, D is twice the maximal radius or circumradius, R, which equals the side length, t. The minimal diameter or the diameter of the inscribed circle (separation of parallel sides, flat-to-flat distance, or height when resting on a flat base), d, is twice the minimal radius or inradius, r. The maxima and minima are related by the same factor:

${\displaystyle {\frac {1}{2}}d=r=\cos(30^{\circ })R={\frac {\sqrt {3}}{2}}R}$     and, similarly, ${\displaystyle d={\frac {\sqrt {3}}{2}}D}$

The area of a regular hexagon

${\displaystyle {\begin{aligned}A&={\frac {3{\sqrt {3}}}{2}}R^{2}=3Rr=2{\sqrt {3}}r^{2}\\&={\frac {3{\sqrt {3}}}{8}}D^{2}={\frac {3}{4}}Dd={\frac {\sqrt {3}}{2}}d^{2}\\&\approx 2.598R^{2}\approx 3.464r^{2}\\&\approx 0.6495D^{2}\approx 0.866d^{2}.\end{aligned}}}$

For any regular polygon, the area can also be expressed in terms of the apothem, a = r, and perimeter, p${\displaystyle {}=6R=4r{\sqrt {3}}}$:

${\displaystyle {\begin{aligned}A&={\frac {ap}{2}}\\&={\frac {r\cdot 4r{\sqrt {3}}}{2}}=2r^{2}{\sqrt {3}}\\&\approx 3.464r^{2},\end{aligned}}}$

The regular hexagon fills the fraction ${\displaystyle {\tfrac {3{\sqrt {3}}}{2\pi }}\approx 0.8270}$ of its circumscribed circle.
If a regular hexagon has successive vertices A, B, C, D, E, F and if P is any point on the circumscribing circle between B and C, then PE + PF = PA + PB + PC + PD.

Symmetry[edit]

The six lines of reflection of a regular hexagon, with Dih₆ or r12 symmetry, order 12.

The dihedral symmetries are divided depending on whether they pass through vertices (d for diagonal) or edges (p for perpendiculars) Cyclic symmetries in the middle column are labeled as g for their central gyration orders. Full symmetry of the regular form is r12 and no symmetry is labeled a1.

The regular hexagon has Dih₆ symmetry, order 12. There are 3 dihedral subgroups: Dih₃, Dih₂, and Dih₁, and 4 cyclic subgroups: Z₆, Z₃, Z₂, and Z₁.
These symmetries express 9 distinct symmetries of a regular hexagon. John Conway labels these by a letter and group order.^[2] r12 is full symmetry, and a1 is no symmetry. d6, a isogonal hexagon constructed by four mirrors can alternate long and short edges, and p6, an isotoxal hexagon constructed with equal edge lengths, but vertices alternating two different internal angles. These two forms are duals of each other and have half the symmetry order of the regular hexagon. The i4 forms are regular hexagons flattened or stretched along one symmetry direction. It can be seen as an elongated rhombus, while d2 and p2 can be seen as horizontally and vertically elongated kites. g2 hexagons, with opposite sides parallel are also called hexagonal parallelogons.
Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g6 subgroup has no degrees of freedom but can seen as directed edges.