(Click
here for Part 1.)
A common argument for the use of technology is that it frees students from doing boring, tedious calculations, and they can focus attention on more interesting and stimulating conceptual matters. This is wrong. Mastering “tedious” calculations frequently goes hand-in-hand with a deep connection with important mathematical
ideas. And that is what mathematics is all about, is it not?
The desire to free students from boring technical matters is a false dichotomy: Mastering technique and deep conceptual understanding go hand-in-hand, and there is absolutely no reason why one can’t work on both in tandem. This is what music students do: To learn to play a musical instrument, one must spend a certain amount of time
every day on theory and technique, and a certain amount of time
every day practicing pieces of music, developing musicality, and so on. Trying to take a short-cut by not doing scales every day is deadly for a music student; can’t we see that the same kind of short-cut is deadly for a mathematics student, too?
A case in point is some of the algorithms we used to learn 40-odd years ago that have now been relegated to the slag heap. For instance, when I was in high-school (could it have been elementary school?) I learned an algorithm for extracting the square root of a number; nowadays, this is never taught, because we can quickly determine the result to many decimal places with hand-calculators, which were not available to students or teachers back then. Another example is the use of trigonometric tables. But the example I want to talk about in this post is the use of logarithm and anti-logarithm tables to facilitate the multiplication, division, and exponentiation of numbers, particularly large numbers.
So take yourself back, back, back, … back to a time when little me and my little classmates had no hand calculators. Let me show you the technique we learned to multiply large numbers, and then we’ll make a connection to higher mathematics.
The technique depends on a property of logarithms:
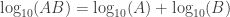
Suppose little 1973 me had the task of multiplying 18793.26 by 54778.18. Using the multiplication algorithm would take a bit of time, but it’s feasible. But here is the time-saving technique we were taught: Let
A = 18793.26 and let
B = 54778.18. Now look up the logarithm of each of the numbers from a table. (Back then we would have relied on tables in the back of our textbooks, but the only book on my shelf that has such tables is my 1971 copy of the CRC Standard Mathematical Tables, 19th edition. The upcoming 2011 edition is
here.)
Reading from the table for figures close to
A:
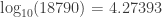
and
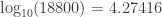
Now if we linearly interpolate between these two figures, for greater accuracy, we obtain the approximation
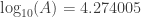
Reading from the table for figures close to
B:
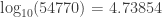
and
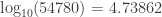
Now if we linearly interpolate between these two figures, for greater accuracy, we obtain the approximation
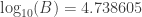
Next, we use the property of logarithms mentioned earlier to estimate the logarithm of
AB:
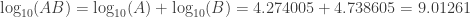
The process of adding logarithms is
very easy, and this is the point of the method. We’ve taken a relatively complicated problem (multiplying two numbers that have many digits) and converted it to a much easier problem (adding two numbers that have many digits). Now we have to convert the result back into the realm of the initial problem.
Next, we convert

to exponential form:
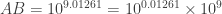
Using a table of “anti-logarithms,” as they were called back then (i.e., a table of powers of 10), we read that:

and

Interpolating again, we get the approximation that

Using a hand calculator, the result is
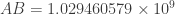
so the approximation using logarithms is correct to four significant figures.
The only way to really appreciate how much work is saved using logarithms is to actually multiply
A and
B by hand.
Besides the value in taking a little trip down memory lane (which is always useful for students, to inform them about how things were done in the past), there is a more general lesson that one can take from this little calculation technique.
IDEA: If you are having difficulty solving a mathematics problem, see if it is possible to transfer the problem into a different realm, where it is easier to solve a related problem, and then transfer the result back into the initial realm to obtain the solution to the original problem.
This is a valuable problem-solving idea. Another example of this idea is the use of
Laplace transforms in solving certain differential equations. The idea is to convert a differential equation into an algebraic equation, solve the algebraic equation (which is easier than solving the differential equation directly), and then use an inverse transform to convert the resulting algebraic expression back into the realm of the original problem.
Pedagogically, it’s very useful to have the logarithm example of this post in your back pocket before you encounter Laplace transforms; once you realize they are both instances of the same basic idea, it helps you to understand the big picture in which Laplace transforms are writ, and it helps you to get the hang of the Laplace transform method.
There are lots of other instances of the same basic idea. There are lots of other
integral transforms (
Fourier transforms are just one type), and in
signal processing one frequently switches back and forth from the time domain to the frequency domain. Integral transforms are also used in the computer software that converts raw data from
medical imaging devices to the lovely images that doctors then peruse. The same ideas are used in analyzing
crystal structure using X-ray diffraction, and more generally in quantum mechanics one often switches from configuration-space representations to momentum-space representations. (The crystallographers speak of “space” and “
reciprocal space,” and also reciprocal basis, and reciprocal lattice.)
One also encounters the same idea in a technique for solving troublesome real improper integrals: One switches to the complex domain, evaluates a related
contour integral using the techniques of
complex analysis, then switches back to the real line to evaluate the real integral.
Back to the technique described in this post. The same idea can also be used to divide numbers with many digits, and to raise a number to another number; one just uses the appropriate properties of logarithms. Try it for yourself and see if you can get this to work!