Points, cones and catastrophe surfaces........

Conic section

From Wikipedia, the free encyclopedia

Jump to: navigation, search

Types of conic sections:
1. Parabola
2. Circle and ellipse
3. Hyperbola

Table of conics, Cyclopaedia, 1728

In mathematics, a conic section (or simply conic) is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse. The circle is a special case of the ellipse, and is of sufficient interest in its own right that it was sometimes called a fourth type of conic section. The conic sections have been studied by the ancient Greek mathematicians with this work culminating around 200 BC, when Apollonius of Perga undertook a systematic study of their properties.
The conic sections of the Euclidean plane have many distinguishing properties. Many of these have been used as the basis for a definition of the conic sections. One such property defines a non-circular conic^[1] to be the set of those points whose distances to some particular point, called a focus, and some particular line, called a directrix, are in a fixed ratio, called the eccentricity. The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2; that is, as the set of points whose coordinates satisfy a quadratic equation in two variables. This equation may be written in matrix form, and some geometric properties can be studied as algebraic conditions.
In the Euclidean plane, the conic sections appear to be quite different from one another, but share many properties. By extending the geometry to a projective plane (adding a line at infinity) this apparent difference vanishes, and the commonality becomes evident. Further extension, by expanding the real coordinates to admit complex coordinates, provides the means to see this unification algebraically.

Contents

 [hide] 

• 1 Euclidean geometry
  • 1.1 Definition
  • 1.2 Eccentricity, focus and directrix
  • 1.3 Conic parameters
  • 1.4 Standard forms in Cartesian coordinates
  • 1.5 General Cartesian form
    • 1.5.1 Matrix notation
    • 1.5.2 Discriminant
    • 1.5.3 Invariants
    • 1.5.4 Eccentricity in terms of coefficients
    • 1.5.5 Conversion to canonical form
  • 1.6 Polar coordinates
  • 1.7 Properties
• 2 History
  • 2.1 Menaechmus and early works
  • 2.2 Apollonius of Perga
  • 2.3 Al-Kuhi
  • 2.4 Omar Khayyám
  • 2.5 Europe
• 3 Applications
• 4 In the real projective plane
  • 4.1 Intersection at infinity
  • 4.2 Homogeneous coordinates
  • 4.3 Projective definition of a circle
  • 4.4 Steiner's projective conic definition
  • 4.5 Line conics
  • 4.6 Von Staudt's definition
  • 4.7 Constructions
• 5 In the complex projective plane
• 6 Degenerate cases
• 7 Pencil of conics
• 8 Intersecting two conics
• 9 Generalizations
• 10 In other areas of mathematics
• 11 See also
• 12 Notes
• 13 References
• 14 External links

Euclidean geometry

The conic sections have been studied for thousands of years and have provided a rich source of interesting and beautiful results in Euclidean geometry.

Definition

The black boundaries of the colored regions are conic sections.

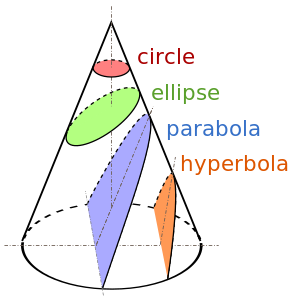
A conic is the curve obtained as the intersection of a plane, called the cutting plane, with the surface of a double cone (a cone with two nappes). We shall assume that the cone is a right circular cone for the purpose of easy description, but this is not required; any double cone with some circular cross-section will suffice. Planes that pass through the vertex of the cone will intersect the cone in a point, a line or a pair of intersecting lines. These are called degenerate conics and some authors do not consider them to be conics at all. Unless otherwise stated, we shall assume that "conic" refers to a non-degenerate conic.
There are three types of conics, the ellipse, parabola, and hyperbola. The circle is a special kind of ellipse, although historically it had been considered as a fourth type (as it was by Apollonius). The circle and the ellipse arise when the intersection of the cone and plane is a closed curve. The circle is obtained when the cutting plane is parallel to the plane of the generating circle of the cone – for a right cone, see diagram, this means that the cutting plane is perpendicular to the symmetry axis of the cone. If the cutting plane is parallel to exactly one generating line of the cone, then the conic is unbounded and is called a parabola. In the remaining case, the figure is a hyperbola. In this case, the plane will intersect both halves of the cone, producing two separate unbounded curves.

Eccentricity, focus and directrix

Ellipse (e=1/2), parabola (e=1) and hyperbola (e=2) with fixed focus F and directrix (e=∞).

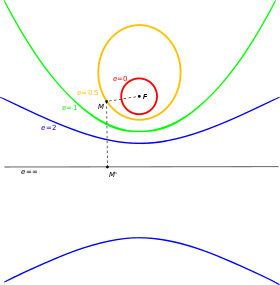
A property that the conic sections share is often presented as the following definition. A conic section is the locus of all points P whose distance to a fixed point F (called the focus of the conic) is a constant multiple (called the eccentricity, e) of the distance from P to a fixed line L (called the directrix of the conic). For 0 < e < 1 we obtain an ellipse, for e = 1 a parabola, and for e > 1 a hyperbola.
A circle is a limiting case and is not defined by a focus and directrix, in the plane (however, see the section on the extension to projective planes). The eccentricity of a circle is defined to be zero and its focus is the center of the circle, but there is no line in the Euclidean plane that is its directrix.^[2]
An ellipse and a hyperbola each have two foci and distinct directrices for each of them. The line joining the foci is called the principal axis and the points of intersection of the conic with the principal axis are called the vertices of the conic. The line segment joining the vertices of a conic is called the major axis, also called transverse axis in the hyperbola. The midpoint of this line segment is called the center of the conic.^[3] Let a denote the distance from the center to a vertex of an ellipse or hyperbola. The distance from the center to a directrix is a/e while the distance from the center to a focus is ae.^[4]
A parabola does not have a center.
The eccentricity of an ellipse can be seen as a measure of how far the ellipse deviates from being circular.
A proof that the conic sections given by the focus-directrix property are the same as those given by planes intersecting a cone is facilitated by the use of Dandelin spheres.^[5]

Conic parameters

Conic parameters in the case of an ellipse

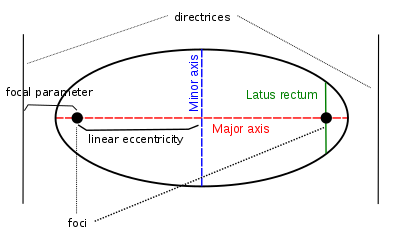
Various parameters are associated with a conic section. Recall that the principal axis is the line joining the foci of an ellipse or hyperbola, and the center in these cases is the midpoint of the line segment joining the foci. Some of the other common features and/or parameters of conics are given below.
The linear eccentricity (c) is the distance between the center and the focus (or one of the two foci).
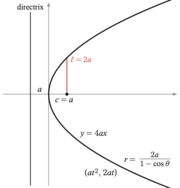
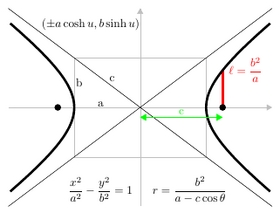
The latus rectum is the chord parallel to the directrix and passing through the focus (or one of the two foci). Its length is denoted by 2ℓ.
The semi-latus rectum (ℓ) is half of the length of the latus rectum.
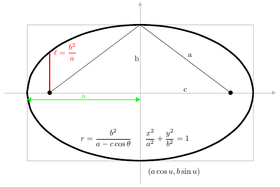
The focal parameter (p) is the distance from the focus (or one of the two foci) to the directrix.
When an ellipse or hyperbola are in standard position (the principle axis is the x-axis and the center is the origin) the vertices of the conic have coordinates (−a, 0) and (a,0), with a non-negative.
The semi-major axis is the value a.
The semi-minor axis is the value b in the standard Cartesian equation of the ellipse or hyperbola.
The following relations hold:

• ${\displaystyle pe=\ell \,}$
• ${\displaystyle ae=c.\,}$

These parameters are related as shown in the following table, where the standard position is assumed. In all cases, a and b are positive.

conic section	equation	eccentricity (e)	linear eccentricity (c)	semi-latus rectum (ℓ)	focal parameter (p)
circle	${\displaystyle x^{2}+y^{2}=a^{2}\,}$	${\displaystyle 0\,}$	${\displaystyle 0\,}$	${\displaystyle a\,}$	${\displaystyle \infty }$
ellipse	${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}$	${\displaystyle {\sqrt {1-{\frac {b^{2}}{a^{2}}}}}}$	${\displaystyle {\sqrt {a^{2}-b^{2}}}}$	${\displaystyle {\frac {b^{2}}{a}}}$	${\displaystyle {\frac {b^{2}}{\sqrt {a^{2}-b^{2}}}}}$
parabola	${\displaystyle y^{2}=4ax\,}$	${\displaystyle 1\,}$	N/A	${\displaystyle 2a\,}$	${\displaystyle 2a\,}$
hyperbola	${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$	${\displaystyle {\sqrt {1+{\frac {b^{2}}{a^{2}}}}}}$	${\displaystyle {\sqrt {a^{2}+b^{2}}}}$	${\displaystyle {\frac {b^{2}}{a}}}$	${\displaystyle {\frac {b^{2}}{\sqrt {a^{2}+b^{2}}}}}$

Standard forms in Cartesian coordinates

Standard forms of an ellipse

Standard forms of a parabola

Standard forms of a hyperbola

After introducing Cartesian coordinates the focus-directrix property can be used to produce equations that the coordinates of the points of the conic section must satisfy.^[6] By means of a change of coordinates (a rotation of axes and a translation of axes) these equations can be put into standard forms.^[7] For ellipses and (general) hyperbolas a standard form would have the x-axis as the principal axis and the origin (the point (0,0)) as the center. The vertices would have coordinates (±a, 0) and foci coordinates (±c,0). Define b by the equations c² = a² − b² for an ellipse and c² = a² + b² for a hyperbola. For a circle, c = 0 so a² = b². For the parabola, the standard form has the focus on the x-axis at the point (a, 0) and the directrix the line with equation x = −a. In standard form the parabola will always pass through the origin. A special case of the hyperbola occurs when its asymptotes are perpendicular. This special case is called a rectangular or equilateral hyperbola. In this case, the standard form is obtained by taking the asymptotes as the coordinate axes and the line x = y as the principal axis. The foci would have coordinates (c, c) and (−c, −c).^[8]

• Circle: x² + y² = a²
• Ellipse: x²/a² + y²/b² = 1
• Parabola: y² = 4ax with a > 0
• Hyperbola: x²/a² − y²/b² = 1
• Rectangular hyperbola:^[9] xy = c²/2

The first four of these forms are symmetric about both the x-axis and y-axis (for the circle, ellipse and hyperbola), or about the x-axis only (for the parabola). The rectangular hyperbola, however, is instead symmetric about the lines y = x and y = −x.
These standard forms can be written parametrically as,

• Circle: (a cos θ, a sin θ),
• Ellipse: (a cos θ, b sin θ),
• Parabola: (at², 2at),
• Hyperbola: (a sec θ, b tan θ) or (±a cosh u, b sinh u),
• Rectangular hyperbola: (dt , d/t) where d = c/√2.

General Cartesian form

In the Cartesian coordinate system, the graph of a quadratic equation in two variables is always a conic section (though it may be degenerate^[10]), and all conic sections arise in this way. The most general equation is of the form^[11]

${\displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0,}$

with all coefficients real numbers and A, B, C not all zero.

Matrix notation

Main article: Matrix representation of conic sections

The above equation can be written in matrix notation as^[12]

${\displaystyle \left({\begin{matrix}x&y\end{matrix}}\right)\left({\begin{matrix}A&B/2\\B/2&C\end{matrix}}\right)\left({\begin{matrix}x\\y\end{matrix}}\right)+\left({\begin{matrix}D&E\end{matrix}}\right)\left({\begin{matrix}x\\y\end{matrix}}\right)+F=0.}$

The general equation can also be written as

${\displaystyle \left({\begin{matrix}x&y&1\end{matrix}}\right)\left({\begin{matrix}A&B/2&D/2\\B/2&C&E/2\\D/2&E/2&F\end{matrix}}\right)\left({\begin{matrix}x\\y\\1\end{matrix}}\right)=0.}$

This form is a specialization of the homogeneous form used in the more general setting of projective geometry (see below).

Discriminant

The conic sections described by this equation can be classified by the discriminant of the equation:^[13]

${\displaystyle B^{2}-4AC.}$

Thus, the discriminant is −4Δ where Δ is the matrix determinant ${\displaystyle \left|{\begin{matrix}A&B/2\\B/2&C\end{matrix}}\right|.}$
If the conic is non-degenerate, then:^[14]

• if B² - 4AC < 0, the equation represents an ellipse;
  • if A = C and B = 0, the equation represents a circle, which is a special case of an ellipse;
• if B² - 4AC = 0, the equation represents a parabola;
• if B² - 4AC > 0, the equation represents a hyperbola;
  • if we also have A + C = 0, the equation represents a rectangular hyperbola.

In the notation used here, A and B are polynomial coefficients, in contrast to some sources that denote the semimajor and semiminor axes as A and B.

Invariants

The discriminant B²–4AC of the conic section's quadratic equation (or equivalently the determinant AC–B²/4 of the 2×2 matrix) and the quantity A + C (the trace of the 2×2 matrix) are invariant under