Logarithmic integral function
From Wikipedia, the free encyclopedia
In mathematics, the logarithmic integral function or integral logarithm li ( x) is a special function. It is relevant in problems of physics and has number theoretic significance, occurring in the prime number theorem as an estimate of the number of prime numbers less than a given value.
Contents
[
Integral representation[ edit]
The logarithmic integral has an integral representation defined for all positive real numbers x ≠ 1 by the definite integral:
Here, ln denotes the natural logarithm. The function  has a singularity at t = 1, and the integral
has a singularity at t = 1, and the integral for x > 1 has to be interpreted as a Cauchy principal value:
 has a singularity at t = 1, and the integral
has a singularity at t = 1, and the integral
Offset logarithmic integral[ edit]
The offset logarithmic integral or Eulerian logarithmic integral is defined as
As such, the integral representation has the advantage of avoiding the singularity in the domain of integration.
This function is a very good approximation to the number of prime numbers less than x.
Series representation[ edit]
Special values[ edit]
The function li ( x) has a single positive zero; it occurs at x ≈ 1.45136 92348 ...  A070769; this number is known as the Ramanujan–Soldner constant.
A070769; this number is known as the Ramanujan–Soldner constant.
This is  where
where  is the incomplete gamma function. It must be understood as the Cauchy principal value of the function.
is the incomplete gamma function. It must be understood as the Cauchy principal value of the function.
 where
where  is the incomplete gamma function. It must be understood as the Cauchy principal value of the function.
is the incomplete gamma function. It must be understood as the Cauchy principal value of the function.
Asymptotic expansion[ edit]
The asymptotic behavior for x → ∞ is
This gives the following more accurate asymptotic behaviour :
Note that, as an asymptotic expansion, this series is not convergent: it is a reasonable approximation only if the series is truncated at a finite number of terms, and only large values of x are employed. This expansion follows directly from the asymptotic expansion for the exponential integral.
Number theoretic significance[ edit]
The logarithmic integral is important in number theory, appearing in estimates of the number of prime numbers less than a given value. For example, the prime number theorem states that:
 denotes the number of primes smaller than or equal to
denotes the number of primes smaller than or equal to



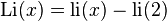
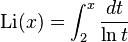


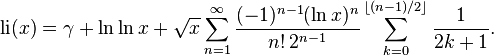

 is the
is the 



No comments:
Post a Comment