Diff types of curves............only the ellipse can have an ecc. = 1/2.........................


Eccentricity, focus and directrix

Ellipse (e=1/2), parabola (e=1) and hyperbola (e=2) with fixed focus F and directrix (e=∞).

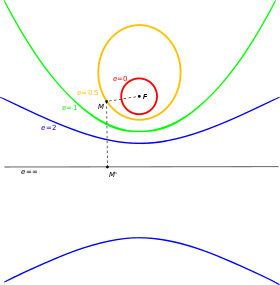
A property that the conic sections share is often presented as the following definition. A conic section is the locus of all points P whose distance to a fixed point F (called the focus of the conic) is a constant multiple (called the eccentricity, e) of the distance from P to a fixed line L (called the directrix of the conic). For 0 < e < 1 we obtain an ellipse, for e = 1 a parabola, and for e > 1 a hyperbola.