The basic parts of math are connected............and have connections to physics.............and beyond.....


Eccentricity, focus and directrix

Ellipse (e=1/2), parabola (e=1) and hyperbola (e=2) with fixed focus F and directrix (e=∞).

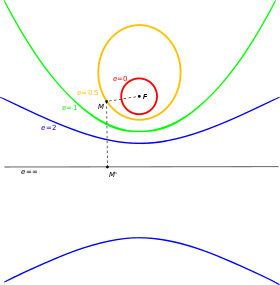
A property that the conic sections share is often presented as the following definition. A conic section is the locus of all points P whose distance to a fixed point F (called the focus of the conic) is a constant multiple (called the eccentricity, e) of the distance from P to a fixed line L (called the directrix of the conic). For 0 < e < 1 we obtain an ellipse, for e = 1 a parabola, and for e > 1 a hyperbola.
A circle is a limiting case and is not defined by a focus and directrix, in the plane (however, see the section on the extension to projective planes). The eccentricity of a circle is defined to be zero and its focus is the center of the circle, but there is no line in the Euclidean plane that is its directrix.^[2]
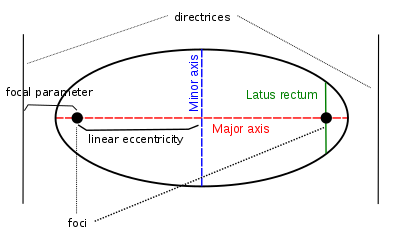
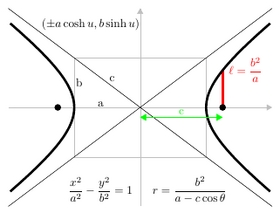
An ellipse and a hyperbola each have two foci and distinct directrices for each of them. The line joining the foci is called the principal axis and the points of intersection of the conic with the principal axis are called the vertices of the conic. The line segment joining the vertices of a conic is called the major axis, also called transverse axis in the hyperbola. The midpoint of this line segment is called the center of the conic.^[3] Let a denote the distance from the center to a vertex of an ellipse or hyperbola. The distance from the center to a directrix is a/e while the distance from the center to a focus is ae.^[4]
A parabola does not have a center.
The eccentricity of an ellipse can be seen as a measure of how far the ellipse deviates from being circular.
A proof that the conic sections given by the focus-directrix property are the same as those given by planes intersecting a cone is facilitated by the use of Dandelin spheres.^[5]

Conic parameters

Conic parameters in the case of an ellipse

Various parameters are associated with a conic section. Recall that the principal axis is the line joining the foci of an ellipse or hyperbola, and the center in these cases is the midpoint of the line segment joining the foci. Some of the other common features and/or parameters of conics are given below.
The linear eccentricity (c) is the distance between the center and the focus (or one of the two foci).
The latus rectum is the chord parallel to the directrix and passing through the focus (or one of the two foci). Its length is denoted by 2ℓ.
The semi-latus rectum (ℓ) is half of the length of the latus rectum.
The focal parameter (p) is the distance from the focus (or one of the two foci) to the directrix.
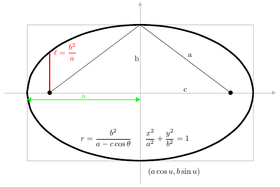
When an ellipse or hyperbola are in standard position (the principle axis is the x-axis and the center is the origin) the vertices of the conic have coordinates (−a, 0) and (a,0), with a non-negative.
The semi-major axis is the value a.
The semi-minor axis is the value b in the standard Cartesian equation of the ellipse or hyperbola.
The following relations hold:

• ${\displaystyle pe=\ell \,}$
• ${\displaystyle ae=c.\,}$

These parameters are related as shown in the following table, where the standard position is assumed. In all cases, a and b are positive.

conic section	equation	eccentricity (e)	linear eccentricity (c)	semi-latus rectum (ℓ)	focal parameter (p)
circle	${\displaystyle x^{2}+y^{2}=a^{2}\,}$	${\displaystyle 0\,}$	${\displaystyle 0\,}$	${\displaystyle a\,}$	${\displaystyle \infty }$
ellipse	${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}$	${\displaystyle {\sqrt {1-{\frac {b^{2}}{a^{2}}}}}}$	${\displaystyle {\sqrt {a^{2}-b^{2}}}}$	${\displaystyle {\frac {b^{2}}{a}}}$	${\displaystyle {\frac {b^{2}}{\sqrt {a^{2}-b^{2}}}}}$
parabola	${\displaystyle y^{2}=4ax\,}$	${\displaystyle 1\,}$	N/A	${\displaystyle 2a\,}$	${\displaystyle 2a\,}$
hyperbola	${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$	${\displaystyle {\sqrt {1+{\frac {b^{2}}{a^{2}}}}}}$	${\displaystyle {\sqrt {a^{2}+b^{2}}}}$	${\displaystyle {\frac {b^{2}}{a}}}$	${\displaystyle {\frac {b^{2}}{\sqrt {a^{2}+b^{2}}}}}$

Standard forms in Cartesian coordinates

Standard forms of an ellipse

Standard forms of a parabola

Standard forms of a hyperbola

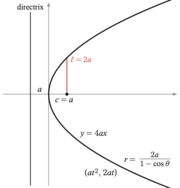
After introducing Cartesian coordinates the focus-directrix property can be used to produce equations that the coordinates of the points of the conic section must satisfy.^[6] By means of a change of coordinates (a rotation of axes and a translation of axes) these equations can be put into standard forms.^[7] For ellipses and (general) hyperbolas a standard form would have the x-axis as the principal axis and the origin (the point (0,0)) as the center. The vertices would have coordinates (±a, 0) and foci coordinates (±c,0). Define b by the equations c² = a² − b² for an ellipse and c² = a² + b² for a hyperbola. For a circle, c = 0 so a² = b². For the parabola, the standard form has the focus on the x-axis at the point (a, 0) and the directrix the line with equation x = −a. In standard form the parabola will always pass through the origin. A special case of the hyperbola occurs when its asymptotes are perpendicular. This special case is called a rectangular or equilateral hyperbola. In this case, the standard form is obtained by taking the asymptotes as the coordinate axes and the line x = y as the principal axis. The foci would have coordinates (c, c) and (−c, −c).^[8]

• Circle: x² + y² = a²
• Ellipse: x²/a² + y²/b² = 1
• Parabola: y² = 4ax with a > 0
• Hyperbola: x²/a² − y²/b² = 1
• Rectangular hyperbola:^[9] xy = c²/2