Why?  If u took it literally.....in different directions.......................in the imaginary direction...........b/c the length of the radius is the same.......it is a circle after all...............would all be a distance of 1/2....but up, north.....the radius would be 1/2i..................to the right and left......along the X axis it would be 1/2......real units......south...........- 1/2i..............

Complex Plane

	No, not that complex plane ...
...  this complex plane:	A plane for complex numbers!

(Also called an "Argand Diagram")

Real and Imaginary make Complex

A Complex Number is a combination of a Real Number and an Imaginary Number:

A Real Number is the type of number we use every day.
Examples: 12.38, ½, 0, −2000

When we square a Real Number we get a positive (or zero) result:

2² = 2 × 2 = 4
1² = 1 × 1 = 1
0² = 0 × 0 = 0

What can we square to get −1?

?² = −1

Squaring −1 does not work because multiplying negatives gives a positive: (−1) × (−1) = +1, and no other Real Number works either.

So it seems that mathematics is incomplete ... 

... but we can fill the gap by imagining there is a number that, when multiplied by itself, gives −1
(call it i for imaginary):

i² = −1

An Imaginary Number, when squared gives a negative result

.

Examples: 5i, -3.6i, i/2, 500i

And together:

A Complex Number is a combination of a Real Number and an Imaginary Number
Examples: 3.6 + 4i, −0.02 + 1.2i, 25 − 0.3i, 0 + 2i

Putting a Complex on a Plane

You may be familiar with the number line:

But where do we put a complex number like 3+4i ?

Let's have the real number line go left-right as usual, and have the  imaginary number line go up-and-down:

We can then plot a complex number like 3 + 4i : It is placed 3 units along (the real axis),  and 4 units up (the imaginary axis).
And here is  4 - 2i : It is placed 4 units along (the real axis),  and 2 units down (the imaginary axis).

And that is the complex plane:

• complex because it is a combination of real and imaginary, 
• plane because it is like a geometric plane (2 dimensional).

Whole New World

Now we can bring the idea of a plane (Cartesian coordinates, Polar coordinates, Vectors etc) to complex numbers, and open up a whole new world of numbers that are more complete and elegant, as you will see.

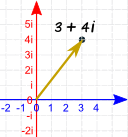
Complex Number as a Vector

We can think of a complex number as a vector.

This is a vector.
It has magnitude (length) and direction.

And here is the complex number 3 + 4i as a Vector:

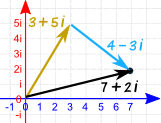
You can add complex numbers as vectors, too:

To add the complex numbers 3 + 5i and  4 − 3i : add the real numbers, and add the imaginary numbers separately like this: (3 + 5i) + (4 − 3i) = 3 + 4 + (5 − 3)i = 7 + 2i

Polar Form

Let's use 3 + 4i again:
Here it is in polar form: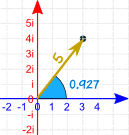

So the complex number 3 + 4i can also be shown as distance (5) and angle (0.927 radians).

Let's see how to convert from one form to the other using Cartesian to Polar conversion: 

Example: the number 3 + 4i

From 3 + 4i :

• r = √(x² + y²) = √(3² + 4²) = √25 = 5
• θ = tan^-1 (y/x) = tan^-1 (4/3) = 0.927 (to 3 decimals)

And we get distance (5) and angle (0.927 radians)
Back again:

• x = r × cos( θ ) = 5 × cos( 0.927 ) = 5 × 0.6002... = 3 (close enough)
• y = r × sin( θ ) = 5 × sin( 0.927 ) = 5 × 0.7998... = 4 (close enough)

And distance 5 and angle 0.927 becomes 3 and 4 again

In fact a common way to write a complex number in Polar form is

x + iy	=	r cos θ + i r sin θ
	=	r(cos θ + i sin θ)

And "cos θ + i sin θ" is often shortened to "cis θ", so:

x + iy = r cis θ

cis is just shorthand for cos θ + i sin θ

So we can write:

3 + 4i = 5 cis 0.927

In some subjects, like electronics, "cis" is used a lot!

Summary

• The complex plane is a plane with:
  • real numbers running left-right and 
  • imaginary numbers running up-down.
• To convert from Cartesian to Polar Form:
  • r = √(x² + y²)
  • θ = tan^-1 ( y / x )
• To convert from Polar to Cartesian Form:
  • x = r × cos( θ )
  • y = r × sin( θ )
• Polar form r cos θ + i r sin θ is often shortened to r cis θ

Next ... learn about Complex Number Multiplication.