The 45/45 right triangle and the 30/60 right triangles..........seem to play an imp. part in this......
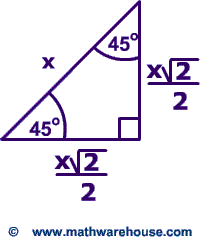
This is one of the 'standard' right triangles you should be able recognize on sight. (Another is the 45-45-90 triangle).
A fact you should commit to memory is:

Read more: http://www.mathwarehouse.com/geometry/triangles/right-triangles/special-right-triangles.php#ixzz5B3xYIzsm
30°- 60°- 90° Triangle
A triangle where the angles are 30°, 60°, and 90°.
Try this In the figure below, drag the orange dots on each vertex to reshape the triangle. Note how the angles remain the same, and it maintains the same proportions between its sides.
A fact you should commit to memory is:
The sides are in the ratio
1
:
2
:
√
3

Notice that the smallest side (1) is opposite the smallest angle (30°), and the longest side (2) is opposite the largest angle (90°). So while writing the ratio as 1: √3 :2 would be more correct, many find the sequence 1: 2: √3 easier to remember, especially when it is spoken. See also Side /angle relationships of a triangle. In the figure above, as you drag the vertices of the triangle to resize it, the angles remain fixed and the sides remain in this ratio.
Corollary
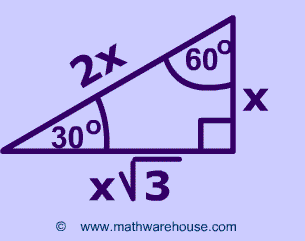
If any triangle has its sides in the ratio 1 - 2 - √3, then it is a 30-60-90 triangle.The 30 60 90 Special Right Triangle
The picture below illustrates the general formula for the 30 60 90 Triangle.General Formula

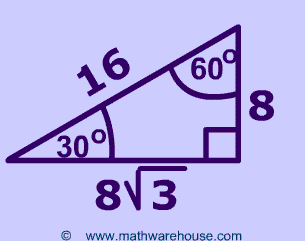
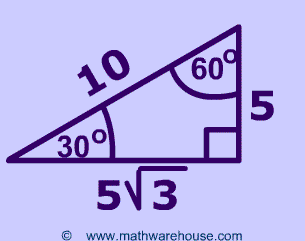
Specific Examples


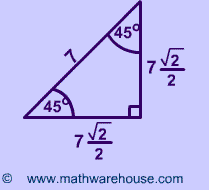
45 45 90 Special Right Triangle

Some Sepcific Examples

Read more: http://www.mathwarehouse.com/geometry/triangles/right-triangles/special-right-triangles.php#ixzz5B3xYIzsm
Comments
Post a Comment