Why was F. Gauss so close???

Riemann's Symphony

One of the great symphonic works of mathematics is the Riemann Hypothesis - humankind's attempt to understand the mysteries of the primes. Each generation has brought its own cultural influences to bear on its understanding of the primes. The themes twist and modulate as we try to master these wild numbers. But this is an unfinished symphony. We still await the mathematician who can add the final chords to this grand opus.

But it isn't just aesthetic similarities that are shared by mathematics and music. Riemann discovered that the physics of music was the key to unlocking the secrets of the primes. He discovered a mysterious harmonic structure that would explain how Gauss's prime number dice actually landed when Nature chose the primes.

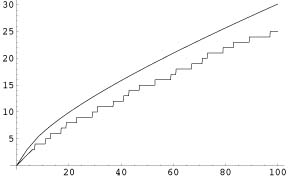
Gauss's function compared to the true number of primes

Riemann was very shy as a schoolchild and preferred to hide in his headmaster's library reading maths books rather than playing outside with his classmates. It was while reading one of these books that Riemann first learnt about Gauss's guess for the number of primes one should encounter as one counts higher and higher. Based on the idea of the prime number dice, Gauss had produced a function, called the logarithmic integral, which seemed to give a very good estimate for the number of primes. The graph to the left shows Gauss's function compared to the true number of primes amongst the first 100 numbers.

Gauss's guess was based on throwing a dice with one side marked "prime" and the others all blank. The number of sides on the dice increases as we test larger numbers and Gauss discovered that the logarithm function could tell him the number of sides needed. For example, to test primes around 1,000 requires a six-sided dice. To make his guess at the number of primes, Gauss assumed that a six-sided dice would land exactly one in six times on the prime side. But of course it is very unlikely that a dice thrown 6,000 times will land exactly 1,000 times on the prime side. A fair dice is allowed to over- or under-estimate this score. But was there any way to understand how to get from Gauss's theoretical guess to the way the prime number dice had really landed? Aged 33, Riemann, now working in Göttingen, discovered that music could explain how to change Gauss's graph into the staircase graph that really counted the primes.