The Cartesian number line goes up by ones..........1, 2, 3, 4, etc.....................and I know not all series do........or numbers.........nor do things always grow by ones............but from an intuitive, general argument..............a series............that gets bigger by ever decreasing numbers.............fractions.........below one...............cannot get bigger than a series..........the number line........which goes up by 1....................

Harmonic series (mathematics)

From Wikipedia, the free encyclopedia

Jump to: navigation, search

Part of a series of articles about
Calculus
Fundamental theorem Limits of functions Continuity Mean value theorem Rolle's theorem
Differential[show] Definitions Derivative (generalizations) Differential infinitesimal of a function total Concepts Differentiation notation Second derivative Third derivative Change of variables Implicit differentiation Related rates Taylor's theorem Rules and identities Sum Product Chain Power Quotient General Leibniz Faà di Bruno's formula
Integral[show] Lists of integrals Definitions Antiderivative Integral (improper) Riemann integral Lebesgue integration Contour integration Integration by Parts Discs Cylindrical shells Substitution (trigonometric) Partial fractions Order Reduction formulae
Series[show] Geometric (arithmetico-geometric) Harmonic Alternating Power Binomial Taylor Convergence tests Summand limit (term test) Ratio Root Integral Direct comparison Limit comparison Alternating series Cauchy condensation Dirichlet Abel
Vector[show] Gradient Divergence Curl Laplacian Directional derivative Identities Theorems Divergence Gradient Green's Kelvin–Stokes
Multivariable[show] Formalisms Matrix Tensor Exterior Geometric Definitions Partial derivative Multiple integral Line integral Surface integral Volume integral Jacobian Hessian matrix
Specialized[show] Fractional Malliavin Stochastic Variations
v t e

In mathematics, the harmonic series is the divergent infinite series:

${\displaystyle \sum _{n=1}^{\infty }\,{\frac {1}{n}}\;\;=\;\;1\,+\,{\frac {1}{2}}\,+\,{\frac {1}{3}}\,+\,{\frac {1}{4}}\,+\,{\frac {1}{5}}\,+\,\cdots .\!}$

Its name derives from the concept of overtones, or harmonics in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength. Every term of the series after the first is the harmonic mean of the neighboring terms; the phrase harmonic mean likewise derives from music.

Contents

 [hide] 

• 1 History
• 2 Paradoxes
• 3 Divergence
  • 3.1 Comparison test
  • 3.2 Integral test
• 4 Rate of divergence
• 5 Partial sums
• 6 Related series
  • 6.1 Alternating harmonic series
  • 6.2 General harmonic series
  • 6.3 p-series
  • 6.4 ln-series
  • 6.5 φ-series
  • 6.6 Random harmonic series
  • 6.7 Depleted harmonic series
• 7 See also
• 8 References
• 9 External links

History[edit]

The fact that the harmonic series diverges was first proven in the 14th century by Nicole Oresme,^[1] but this achievement fell into obscurity. Proofs were given in the 17th century by Pietro Mengoli,^[2] Johann Bernoulli,^[3] and Jacob Bernoulli.^[4]
Historically, harmonic sequences have had a certain popularity with architects. This was so particularly in the Baroque period, when architects used them to establish the proportions of floor plans, of elevations, and to establish harmonic relationships between both interior and exterior architectural details of churches and palaces.^[5]

Paradoxes[edit]

The harmonic series is counterintuitive to students first encountering it, because it is a divergent series even though the limit of the nth term as n goes to infinity is zero. The divergence of the harmonic series is also the source of some apparent paradoxes. One example of these is the "worm on the rubber band".^[6] Suppose that a worm crawls along a 1-metre rubber band at the same time as the rubber band is uniformly stretched. If the worm travels 1 centimetre per minute and the band stretches 1 metre per minute, will the worm ever reach the end of the rubber band? The answer, counterintuitively, is "yes", for after n minutes, the ratio of the distance travelled by the worm to the total length of the rubber band is

${\displaystyle {\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}}$

(In fact the actual ratio is a little less than this sum as the band expands continuously). The reason is that the band expands behind the worm also; eventually, the worm gets past the midway mark and the band behind expands increasingly more rapidly than the band in front.
Because the series gets arbitrarily large as n becomes larger, eventually this ratio must exceed 1, which implies that the worm reaches the end of the rubber band. However, the value of n at which this occurs must be extremely large: approximately e¹⁰⁰, a number exceeding 10⁴³. Although the harmonic series does diverge, it does so very slowly.
Another problem involving the harmonic series is the Jeep problem.

Another example is the block-stacking problem: given a collection of identical dominoes, it is clearly possible to stack them at the edge of a table so that they hang over the edge of the table without falling. The counterintuitive result is that one can stack them in such a way as to make the overhang arbitrarily large, provided there are enough dominoes.^[6][7]
A simpler example, on the other hand, is the swimmer that keeps adding more speed when touching the walls of the pool. The swimmer starts crossing a 10-meter pool at a speed of 2 m/s, and with every cross, another 2 m/s is added to the speed. In theory, the swimmer's speed is unlimited, but the number of pool crosses needed to get to that speed becomes very large; for instance, to get to the speed of light (ignoring special relativity), the swimmer needs to cross the pool 150 million times. Contrary to this large number, the "time" required to reach a given speed depends on the sum of the series at any given number of pool crosses (iterations):

${\displaystyle {\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}.}$

Calculating the sum (iteratively) shows that to get to the speed of light the time required is only 94 seconds. By continuing beyond this point (exceeding the speed of light, again ignoring special relativity), the time taken to cross the pool will in fact approach zero as the number of iterations becomes very large, and although the time required to cross the pool appears to tend to zero (at an infinite number of iterations), the sum of iterations (time taken for total pool crosses) will still diverge at a very slow rate.

Divergence[edit]

There are several well-known proofs of the divergence of the harmonic series. A few of them are given below.

Comparison test[edit]

One way to prove divergence is to compare the harmonic series with another divergent series:

${\displaystyle {\begin{aligned}&1\;\;+\;\;{\frac {1}{2}}\;\;+\;\;{\frac {1}{3}}\,+\,{\frac {1}{4}}\;\;+\;\;{\frac {1}{5}}\,+\,{\frac {1}{6}}\,+\,{\frac {1}{7}}\,+\,{\frac {1}{8}}\;\;+\;\;{\frac {1}{9}}\,+\,\cdots \\[12pt]>\;\;\;&1\;\;+\;\;{\frac {1}{2}}\;\;+\;\;{\frac {1}{4}}\,+\,{\frac {1}{4}}\;\;+\;\;{\frac {1}{8}}\,+\,{\frac {1}{8}}\,+\,{\frac {1}{8}}\,+\,{\frac {1}{8}}\;\;+\;\;{\frac {1}{16}}\,+\,\cdots \end{aligned}}}$

Each term of the harmonic series is greater than or equal to the corresponding term of the second series, and therefore the sum of the harmonic series must be greater than the sum of the second series. However, the sum of the second series is infinite:

${\displaystyle {\begin{aligned}&1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}+{\frac {1}{4}}\right)+\left({\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}\right)+\left({\frac {1}{16}}+\cdots +{\frac {1}{16}}\right)+\cdots \\[12pt]=\;\;&1\;\;+\;\;{\frac {1}{2}}\;\;+\;\;{\frac {1}{2}}\;\;+\;\;{\frac {1}{2}}\;\;+\;\;{\frac {1}{2}}\;\;+\;\;\cdots \;\;=\;\;\infty \end{aligned}}}$

It follows (by the comparison test) that the sum of the harmonic series must be infinite as well. More precisely, the comparison above proves that

${\displaystyle \sum _{n=1}^{2^{k}}\,{\frac {1}{n}}\;\geq \;1+{\frac {k}{2}}}$

for every positive integer k.
This proof, proposed by Nicole Oresme, is considered by many in the mathematical community to be a high point of medieval mathematics. It is still a standard proof taught in mathematics classes today. Cauchy's condensation test is a generalization of this argument.

Integral test[edit]

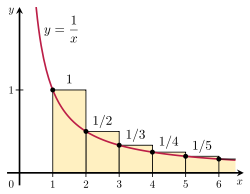
It is possible to prove that the harmonic series diverges by comparing its sum with an improper integral. Specifically, consider the arrangement of rectangles shown in the figure to the right. Each rectangle is 1 unit wide and 1 / n units high, so the total area of the rectangles is the sum of the harmonic series:

${\displaystyle {\begin{array}{c}{\text{area of}}\\{\text{rectangles}}\end{array}}=1\,+\,{\frac {1}{2}}\,+\,{\frac {1}{3}}\,+\,{\frac {1}{4}}\,+\,{\frac {1}{5}}\,+\,\cdots .}$

However, the total area under the curve y = 1 / x from 1 to infinity is given by an improper integral:

${\displaystyle {\begin{array}{c}{\text{area under}}\\{\text{curve}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}\,dx\;=\;\infty .}$