After all, Dr. Evil...........if all "interesting" zeros are on the 1/2 x line.........................which to me they are not....................then what................???  We get nothing.............oh well Dr. Evil.......maybe next time...............

Riemann Hypothesis

 

First published in Riemann's groundbreaking 1859 paper (Riemann 1859), the Riemann hypothesis is a deep mathematical conjecture which states that the nontrivialRiemann zeta function zeros, i.e., the values of 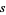 other than 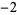, , 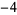, 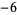... such that  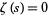(where  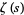is the Riemann zeta function) all lie on the "critical line"  (where  denotes the real part of ).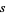

A more general statement known as the generalized Riemann hypothesis conjectures that neither the Riemann zeta function nor any Dirichlet L-series has a zero with real part larger than 1/2.

Legend holds that the copy of Riemann's collected works found in Hurwitz's library after his death would automatically fall open to the page on which the Riemann hypothesis was stated (Edwards 2001, p. ix).

While it was long believed that Riemann's hypothesis was the result of deep intuition on the part of Riemann, an examination of his papers by C. L. Siegel showed that Riemann had made detailed numerical calculations of small zeros of the Riemann zeta function  to several decimal digits (Granville 2002; Borwein and Bailey 2003, p. 68).

The Riemann hypothesis has thus far resisted all attempts to prove it. Stieltjes (1885) published a note claiming to have proved the Mertens conjecture with , a result stronger than the Riemann hypothesis and from which it would have followed. However, the proof itself was never published, nor was it found in Stieltjes papers following his death (Derbyshire 2004, pp. 160-161 and 250). Furthermore, the Mertens conjecture has been proven false, completely invalidating this claim. In the late 1940s, H. Rademacher's erroneous proof of the falsehood of Riemann's hypothesis was reported in Time magazine, even after a flaw in the proof had been unearthed by Siegel (Borwein and Bailey 2003, p. 97; Conrey 2003). de Branges has written a number of papers discussing a potential approach to the generalized Riemann hypothesis (de Branges 1986, 1992, 1994) and in fact claiming to prove the generalized Riemann hypothesis (de Branges 2003, 2004; Boutin 2004), but no actual proofs seem to be present in these papers. Furthermore, Conrey and Li (1998) prove a counterexample to de Branges's approach, which essentially means that theory developed by de Branges is not viable.

Proof of the Riemann hypothesis is number 8 of Hilbert's problems and number 1 of Smale's problems.

In 2000, the Clay Mathematics Institute (http://www.claymath.org/) offered a $1 million prize (http://www.claymath.org/millennium/Rules_etc/) for proof of the Riemann hypothesis. Interestingly, disproof of the Riemann hypothesis (e.g., by using a computer to actually find a zero off the critical line), does not earn the $1 million award.

The Riemann hypothesis was computationally tested and found to be true for the first  zeros by Brent et al. (1982), covering zeros  in the region ). S. Wedeniwski used ZetaGrid (http://www.zetagrid.net/) to prove that the first trillion () nontrivial zeros lie on the critical line. Gourdon (2004) then used a faster method by Odlyzko and Schönhage to verify that the first ten trillion () nontrivial zeros of the  function lie on the critical line. This computation verifies that the Riemann hypothesis is true at least for all  less than 2.4 trillion. These results are summarized in the following table, where  indicates agram point.

		source
		Brent et al. (1982)
		Wedeniwski/ZetaGrid
		Gourdon (2004)

The Riemann hypothesis is equivalent to the statement that all the zeros of the Dirichlet eta function (a.k.a. the alternating zeta function)

(1)

falling in the critical strip  lie on the critical line .

Wiener showed that the prime number theorem is literally equivalent to the assertion that the Riemann zeta function  has no zeros on  (Hardy 1999, pp. 34 and 58-60; Havil 2003, p. 195).

In 1914, Hardy proved that an infinite number of values for  can be found for which  and  (Havil 2003, p. 213). However, it is not known if allnontrivial roots  satisfy . Selberg (1942) showed that a positive proportion of the nontrivial zeros lie on the critical line, and Conrey (1989) proved the fraction to be at least 40% (Havil 2003, p. 213).

André Weil proved the Riemann hypothesis to be true for field functions (Weil 1948, Eichler 1966, Ball and Coxeter 1987). In 1974, Levinson (1974ab) showed that at least 1/3 of the roots must lie on the critical line (Le Lionnais 1983), a result which has since been sharpened to 40% (Vardi 1991, p. 142). It is known that the zeros are symmetrically placed about the line . This follows from the fact that, for all complex numbers ,

1.  and the complex conjugate  are symmetrically placed about this line.