Exponential function
From Wikipedia, the free encyclopedia
This article is about the natural exponential function ex. For the general exponential of the form bx and any base b, see Exponentiation. For exponentially increasing functions of the form cbx, see Exponential growth.
In mathematics, an exponential function is a function of the form
The input variable x occurs as an exponent – hence the name. A function of the form ƒ(x) = bx ± c is also considered an exponential function, and a function of the form ƒ(x) = a·bx can be re-written as ƒ(x) = bx ± c by the use of logarithms and so is an exponential function.
In contexts where the base b is not specified, especially in more theoretical contexts, the term exponential function is almost always understood to mean the natural exponential function
also written as
where e is Euler's number, a transcendental number approximately 2.718281828. The reason this number e is considered the "natural" base of exponential functions is that this function is its own derivative.[1][2] Every exponential function is directly proportional to its own derivative, but only when the base is e does the constant of proportionality equal 1.
The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change (i.e. percentage increase or decrease) in the dependent variable. The function is often written as exp(x), especially when it is impractical to write the independent variable as a superscript. The exponential function is widely used inphysics, chemistry, engineering, mathematical biology, economics and mathematics.
| Representation |  |
| Inverse |  |
| Derivative |  |
| Indefinite Integral |  |
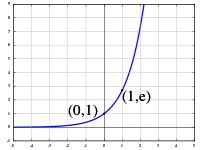
The graph of y = ex is upward-sloping, and increases faster as x increases. The graph always lies above the x-axis but can get arbitrarily close to it for negative x; thus, the x-axis is a horizontal asymptote. The slope of the tangent to the graph at each point is equal to its y coordinate at that point. Theinverse function is the natural logarithm ln(x); because of this, some old texts[3] refer to the exponential function as the antilogarithm.
In general, the variable x can be any real or complex number or even an entirely different kind of mathematical object; see the formal definition below.
| Part of a series of articles on the |
| mathematical constant e |
|---|
 |
| Properties |
|
| Applications |
| Defining e |
| People |
| Related topics |
Contents
[hide]Formal definition[edit]
Main article: Characterizations of the exponential function
The exponential function ex can be characterized in a variety of equivalent ways. In particular it may be defined by the following power series:[4]
Using an alternate definition for the exponential function leads to the same result when expanded as a Taylor series.
Less commonly, ex is defined as the solution y to the equation
It is also the following limit:[5]





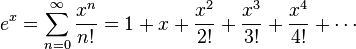


No comments:
Post a Comment