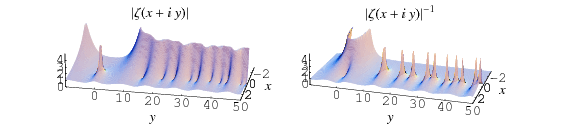
 The figures above highlight the zeros in the complex plane by plotting The figures above highlight the zeros in the complex plane by plotting 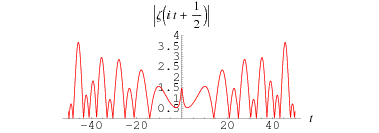 The above plot shows The above plot shows
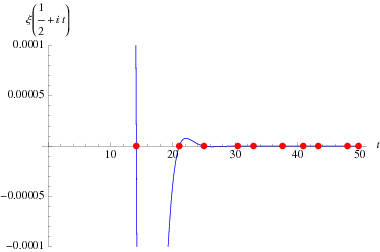 The so-called xi-function The so-called xi-function |
Thursday, March 1, 2018
All that illustrates several imp. numbers/processes, etc..........at once..........overlap for one.........hidden dimensions...............................unfolding.....................14.13i..........14 + 13 = 27...........like e.............without the dec point..............of course adding it like that.........is through a dec point...........and pi....................14.13.............beg to middle........is 14...............end to beg........is 31......overlap the ones..........31 14........it is pi.........314...............pi and e at once........if u add the 1st 3 numbers of e and pi................2.71 + 3.14................= 5.85..........two golden ratios and two 13s.............taken from the middle number............8.................8/5 = 1.6...........8/5 = 1.6...........1.6 + 1.6 = 3.2..................like 2, 3 the start of all primes......but inverted.........5 + 8 = 13..............8 + 5 = 13......................13 + 13 = 26...............1st 25 primes..........words into math (like mathematical logic)............1 + 25 = 26...................
Subscribe to:
Post Comments (Atom)
No comments:
Post a Comment