The 1st "trivial" zero.........is at (-2, 0).............every even neg interger..........from (-2, 0).........to (2, 0)...........is a distance of 4.......along the X axis.....................so if u imagined.............2^i.........two to the i..........i as an exponent............and the way to compute it..........from a conceptual point of view.........i being the square root of - 1..............putting the imag dimen...........to the 3rd d.....from the usual...........2d Cartesian plane..........I graphed all the rest of this................the distance from (2, 0)......to neg one on the X axis is 3..................(2, 0) to (-1, 0)........is 3........or vice versa...............so if u combined the two.......................it is 5.5......which I put before...............yesterday..........2.5 from the 1st "trivial" zero to the critical line......2.5 and 3 being the base of the triangle to compute what 2^i might be......................5.5............................5 * 5 = 25...........like 0.25...........1/4 = 0.25...........1/4th like 14i.....................................5 + 5 = 10................like the 10 base number system..........

Why...........b/c from the 1st zero....trivial zero on the X axis.......to where the critical line crosses the X axis.....is 2.5.................2 from -2, 0......to the origin.......1/2 to the critical line from the origin...............1/2 = 0.5...........so 2.5........from the 1st zero.......on the X axis.....at -2, 0......to the critical line...........and 3...........from 2^i...........they cross........and overlap................without overlap..........it is 4 for the distance..........with overlap..........like hidden dimen...............the unfolded square in Lineland.............etc.........imag stuff in general...............5.5.......which means there is a difference........overlap of 1.5...................the distance the blue lines below are extending........3/2 = 1.5................also imp..........b/c the square root of 13..........= 3.60555.................three 5's.........5 + 5 + 5 = 15.................different parts of the math cannon..........which seem to have nothing to do with one another...........my dad's wording.........not mine.........



The plots above show the real and imaginary parts of plotted in the complex plane together with the complex modulus of . As can be seen, in right half-plane, the function is fairly flat, but with a large number of horizontal ridges. It is precisely along these ridges that the nontrivial zeros of lie.
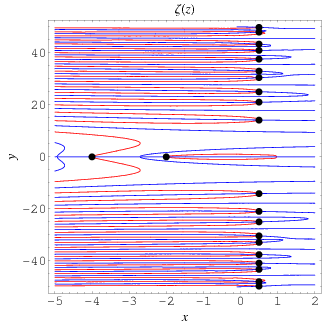
The position of the complex zeros can be seen slightly more easily by plotting the contours of zero real (red) and imaginary (blue) parts, as illustrated above. The zeros (indicated as black dots) occur where the curves intersect.