The 3rd stand dev is different...........just like the 3rd set of 10 numbers....20 - 30.........is different............b/c the 1st 2 sets of 10 numbers..........have 4 primes in them..............the 3rd one........has 2............3 and 2..............41, 43, 47, ...............53, 59............a 3 and a 2............15/10 = 3/2.................the overall distribution of primes matches the specific one.................centered about 50.....from 40 - 60...................20 numbers.........just like the 1st 20 numbers........have 4 and 4 primes.............in them...........when broken in half..........3/2............the 2nd term in E's product................3 + 2 = 5....................5 primes and 5 non primes...10 overall in one of the 2 prime fundamentals...........fractal patterns...............41 is imp................b/c it is the 13 prime..........a garbled pi...............41 and 13.................when the ones are fused together..........like atomic fusion......Albert E.............................

Sym and aysm at once............just like the beg of the primes..........2, 3, 5, 7.............2 and 3..............are the only two primes..........EVER..........to be one digit apart................99%.............different...........the 3rd is different..........just like 20 - 30 is different............in terms of the number of primes in that series....................a 15 year old or so F Gauss saw a pattern in the distribution of primes..............factored by 2..............every even neg number...................on the X axis...........all even numbers..........can be factored by 2.......................like 2pi............full circle...

Why else 40 - 60??  4 and 6.............the 1st two non primes........discounting 0 and 1.........b/c of their spec imp.........I think from some perspectives it IS imp to include them........but for simplicity's sake..............................6.28..................2pi...........the 1st 3 digits of it.........one number above the dec................2 numbers below it.............28/6 = 4.666..........like F's 1st c.............28 - 6 = 22..................2 twos..............2 and 2 - 11............................two prime fund...........there may be more..................

• Home
• Subjects ▼
  • Algebra
  • Calculus
  • Data
  • Geometry
  • Measure
  • Money
  • Numbers
  • Physics
• More ▼
  • Activities
  • Dictionary
  • Games
  • Puzzles
  • Worksheets

 ☰

Normal Distribution

Data can be "distributed" (spread out) in different ways.

It can be spread out more on the left		Or more on the right

Or it can be all jumbled up

But there are many cases where the data tends to be around a central value with no bias left or right, and it gets close to a "Normal Distribution" like this:

A Normal Distribution

The "Bell Curve" is a Normal Distribution.
And the yellow histogram shows some data that
follows it closely, but not perfectly (which is usual).

It is often called a "Bell Curve" because it looks like a bell.

Many things closely follow a Normal Distribution:

• heights of people
• size of things produced by machines
• errors in measurements
• blood pressure
• marks on a test

We say the data is "normally distributed":

The Normal Distribution has:

• mean = median = mode
• symmetry about the center
• 50% of values less than the mean
  and 50% greater than the mean

Quincunx

You can see a normal distribution being created by random chance! It is called the Quincunx and it is an amazing machine. Have a play with it!

Standard Deviations

The Standard Deviation is a measure of how spread out numbers are (read that page for details on how to calculate it).
When we calculate the standard deviation we find that (generally):

68% of values are within 1 standard deviation of the mean 95% of values are within 2 standard deviations of the mean 99.7% of values are within 3 standard deviations of the mean

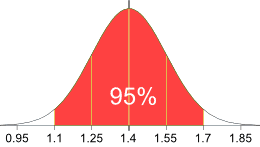
Example: 95% of students at school are between 1.1m and 1.7m tall.

Assuming this data is normally distributed can you calculate the mean and standard deviation?
The mean is halfway between 1.1m and 1.7m:

Mean = (1.1m + 1.7m) / 2 = 1.4m

95% is 2 standard deviations either side of the mean (a total of 4 standard deviations) so:

1 standard deviation	= (1.7m-1.1m) / 4
	= 0.6m / 4
	= 0.15m

And this is the result:

It is good to know the standard deviation, because we can say that any value is: