There is another...........or it seems to me.........

Euler's identity

From Wikipedia, the free encyclopedia

For other uses, see List of topics named after Leonhard Euler § Euler's identities.

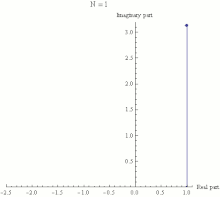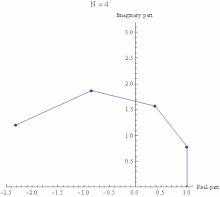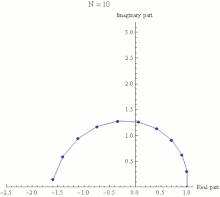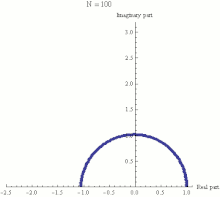
The exponential function e^z can be defined as the limit of (1 + z/N)^N, as Napproaches infinity, and thus e^iπ is the limit of (1 + iπ/N)^N. In this animation Ntakes various increasing values from 1 to 100. The computation of (1 + iπ/N)^N is displayed as the combined effect of Nrepeated multiplications in the complex plane, with the final point being the actual value of (1 + iπ/N)^N. It can be seen that as N gets larger (1 + iπ/N)^Napproaches a limit of −1.

Part of a series of articles on the
mathematical constant e
Properties
Natural logarithm Exponential function
Applications
compound interest Euler's identity Euler's formula half-lives  exponential growth and decay
Defining e
proof that e is irrational representations of e Lindemann–Weierstrass theorem
People
John Napier Leonhard Euler
Related topics
Schanuel's conjecture
v t e

In mathematics, Euler's identity^{[n 1]} (also known as Euler's equation) is the equality

${\displaystyle e^{i\pi }+1=0}$

where

e is Euler's number, the base of natural logarithms,

i is the imaginary unit, which satisfies i² = −1, and

π is pi, the ratio of the circumference of a circle to its diameter.

Euler's identity is named after the Swiss mathematician Leonhard Euler. It is considered to be an example of mathematical beauty.