2, 3..........how all primes start out................and the only instance, ever, where two primes are a digit apart............................they count as both numbers and processes.........

Fibonacci Sequence

The Fibonacci Sequence is the series of numbers:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...

The next number is found by adding up the two numbers before it.

• The 2 is found by adding the two numbers before it (1+1)
• The 3 is found by adding the two numbers before it (1+2),
• And the 5 is (2+3),
• and so on!

Example: the next number in the sequence above is 21+34 = 55

It is that simple!
Here is a longer list:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, ...

Can you figure out the next few numbers?

Makes A Spiral

When we make squares with those widths, we get a nice spiral:

Do you see how the squares fit neatly together?
For example 5 and 8 make 13, 8 and 13 make 21, and so on.

The Rule

The Fibonacci Sequence can be written as a "Rule" (see Sequences and Series).
First, the terms are numbered from 0 onwards like this:

n =	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	...
xn =	0	1	1	2	3	5	8	13	21	34	55	89	144	233	377	...

So term number 6 is called x₆ (which equals 8).

Example: the 8th term is the 7th term plus the 6th term: x8 = x7 + x6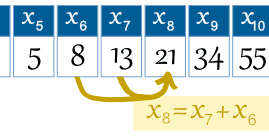

So we can write the rule:

The Rule is x_n = x_n-1 + x_n-2

where:

• x_n is term number "n"
• x_n-1 is the previous term (n-1)
• x_n-2 is the term before that (n-2)

Example: term 9 is calculated like this:

x9	= x9-1 + x9-2
	= x8 + x7
	= 21 + 13
	= 34

Golden Ratio

And here is a surprise. When we take any two successive (one after the other) Fibonacci Numbers, their ratio is very close to the Golden Ratio "φ" which is approximately 1.618034...
In fact, the bigger the pair of Fibonacci Numbers, the closer the approximation. Let us try a few:

A	B		B / A
2	3		1.5
3	5		1.666666666...
5	8		1.6
8	13		1.625
...	...		...
144	233		1.618055556...
233	377		1.618025751...
...	...		...

Note: this also works when we pick two random whole numbers to begin the sequence, such as 192 and 16 (we get the sequence 192, 16, 208, 224, 432, 656, 1088, 1744, 2832, 4576, 7408, 11984, 19392, 31376, ...):

A	B		B / A
192	16		0.08333333...
16	208		13
208	224		1.07692308...
224	432		1.92857143...
...	...		...
7408	11984		1.61771058...
11984	19392		1.61815754...
...	...		...

It takes longer to get good values, but it shows that not just the Fibonacci Sequence can do this!

Using The Golden Ratio to Calculate Fibonacci Numbers

And even more surprising is that we can calculate any Fibonacci Number using the Golden Ratio:

The answer always comes out as a whole number, exactly equal to the addition of the previous two terms.
Example:

When I used a calculator on this (only entering the Golden Ratio to 6 decimal places) I got the answer 8.00000033. A more accurate calculation would be closer to 8.
Try it for yourself!

Some Interesting Things

Here is the Fibonacci sequence again:

n =	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	...
xn =	0	1	1	2	3	5	8	13	21	34	55	89	144	233	377	610	...

There is an interesting pattern:

• Look at the number x₃ = 2. Every 3rd number is a multiple of 2 (2, 8, 34, 144, 610, ...)
• Look at the number x₄ = 3. Every 4th number is a multiple of 3 (3, 21, 144, ...)
• Look at the number x₅ = 5. Every 5th number is a multiple of 5 (5, 55, 610, ...)

And so on (every nth number is a multiple of x_n).

1/89 = 0.011235955056179775...

Notice the first few digits (0,1,1,2,3,5) are the Fibonacci sequence?
In a way they all are, except multiple digit numbers (13, 21, etc) overlap, like this:

0.0
0.01
0.001
0.0002
0.00003
0.000005
0.0000008
0.00000013
0.000000021
... etc ...
0.011235955056179775...  =  1/89

Terms Below Zero

The sequence works below zero also, like this:

n =	...	-6	-5	-4	-3	-2	-1	0	1	2	3	4	5	6	...
xn =	...	-8	5	-3	2	-1	1	0	1	1	2	3	5	8	...

(Prove to yourself that each number is found by adding up the two numbers before it!)

In fact the sequence below zero has the same numbers as the sequence above zero, except they follow a +-+- ... pattern. It can be written like this:

x_−n = (−1)ⁿ⁺¹ x_n

Which says that term "-n" is equal to (−1)ⁿ⁺¹ times term "n", and the value (−1)ⁿ⁺¹ neatly makes the correct 1,-1,1,-1,... pattern.

History

Fibonacci was not the first to know about the sequence, it was known in India hundreds of years before!

About Fibonacci The Man

His real name was Leonardo Pisano Bogollo, and he lived between 1170 and 1250 in Italy.
"Fibonacci" was his nickname, which roughly means "Son of Bonacci".
As well as being famous for the Fibonacci Sequence, he helped spread Hindu-Arabic Numerals (like our present numbers 0,1,2,3,4,5,6,7,8,9) through Europe in place of Roman Numerals (I, II, III, IV, V, etc). That has saved us all a lot of trouble! Thank you Leonardo.

Fibonacci Day

Fibonacci Day is November 23rd, as it has the digits "1, 1, 2, 3" which is part of the sequence. So next Nov 23 let everyone know!