At zero they are also the same.............0 + 0 = 0............0 * 0 = 0...........but between 0 and 2 there are several different things going on..............................................from 0 to 1 is different than 1 to 2.......................adding will give u the a bigger number than multiplying, in either case........................as in 1 + 1 = 2 ............1 * 1 = 1............and u always have to use the same number...............the same number twice........like 1/2.................or 21..........as in 21i..........the location of the 2nd zero............

0 to 1 and 1 to 2 are slightly different.........................1/2 + 1/2 = 1...............1/2 * 1/2 = 1/4..........3/2 + 3/2 = 3...................3/2 * 3/2 = 9/4...........................adding gives u a bigger number than multiplying in either case..........................but the end result from 0 - 1.....................for multiplication........is smaller than the original number..............whereas from 1 - 2............that interval will give u a bigger number than the original.........for multiplying...........................when u are multiplying by a fraction under 1..........u are really dividing........................half of a half is a quarter....................half of 50 cents.......is a quarter.......................1.5 * 1.5 = 2.25.......................2.25 is bigger than 1.5...........adding one and a half to one and a half..........gives u 3......................so adding still gives a bigger number...........but if u multiplied 1/2 * 1/2 = 1/4...............one fourth is smaller than 1/2..........in decimals...........1/4 = 0.25..........1/2 = 0.5........

My point............................amongst other stuff............................near the origin is where things are different...............one of the reasons the Mandel set is the way it is.............




Sums of waves........a crest meeting a trough would cancel each other out.........


The plots above show the real and imaginary parts of plotted in the complex plane together with the complex modulus of . As can be seen, in right half-plane, the function is fairly flat, but with a large number of horizontal ridges. It is precisely along these ridges that the nontrivial zeros of lie.
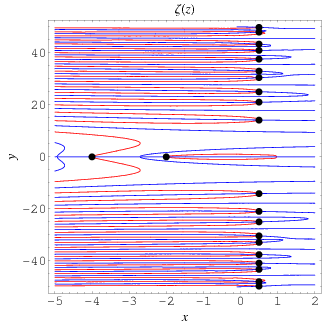
The position of the complex zeros can be seen slightly more easily by plotting the contours of zero real (red) and imaginary (blue) parts, as illustrated above. The zeros (indicated as black dots) occur where the curves intersect.