For extra clarity.........................the difference of squares.....................subtracting the bigger one from the smaller one........using each one twice............save for the 1st one.............as in 1 squared...........

In real numbers[edit]

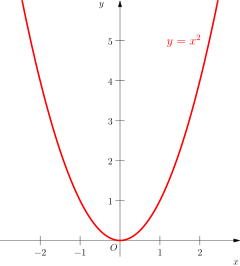
y = x². The graph of a quadratic function has a parabolic shape. The squares of numbers make a power law.

The squaring function preserves the order of positive numbers: larger numbers have larger squares. In other words, squaring is a monotonic function on the interval [0, +∞). On the negative numbers, numbers with greater absolute value have greater squares, so squaring is a monotonically decreasing function on (−∞,0]. Hence, zero is its global minimum. The only cases where the square x² of a number is less than x occur when 0 < x < 1, that is, when x belongs to an open interval (0,1). This implies that the square of an integer is never less than the original number.
Every positive real number is the square of exactly two numbers, one of which is strictly positive and the other of which is strictly negative. Zero is the square of only one number, itself. For this reason, it is possible to define the square root function, which associates with a non-negative real number the non-negative number whose square is the original number.
No square root can be taken of a negative number within the system of real numbers, because squares of all real numbers are non-negative. The lack of real square roots for the negative numbers can be used to expand the real number system to the complex numbers, by postulating the imaginary unit i, which is one of the square roots of −1.
The property "every non negative real number is a square" has been generalized to the notion of a real closed field, which is an ordered field such that every non negative element is a square and every polynomial of odd degree has a root. The real closed fields cannot be distinguished from the field of real numbers by their algebraic properties: every property of the real numbers, which may be expressed in first-order logic (that is expressed by a formula in which the variables that are quantified by ∀ or ∃ represent elements, not sets), is true for every real closed field, and conversely every property of the first-order logic, which is true for a specific real closed field is also true for the real numbers.

In geometry[edit]

There are several major uses of the squaring function in geometry.