Sums of waves........a crest meeting a trough would cancel each other out.........
The plots above show the real and imaginary parts of
plotted in the complex plane together with the complex modulus of 
. As can be seen, in right half-plane, the function is fairly flat, but with a large number of horizontal ridges. It is precisely along these ridges that the nontrivial zeros of 
lie. 
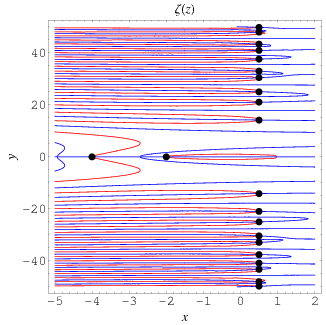
The position of the complex zeros can be seen slightly more easily by plotting the contours of zero real (red) and imaginary (blue) parts, as illustrated above. The zeros (indicated as black dots) occur where the curves intersect.
No comments:
Post a Comment