The ONLY equil triangle.........that can be inscribed in the unit circle...........is a square root of 3 equil triangle...........the ONLY square which can be inscribed in the unit circle.........is the square root of 2 square..............the square root of 2 + the square root of 3 is close to pi......
Yes, yes, it is a pain to have to remember things, but it will make life easier when you know them, not just in exams, but other times when you need to do quick estimates, etc.
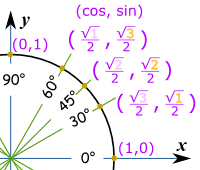 To help you remember, sin goes "1,2,3" :
To help you remember, sin goes "1,2,3" :
And cos goes "3,2,1"
Because they work for both cos and sin:
Pythagoras
Pythagoras' Theorem says that for a right angled triangle, the square of the long side equals the sum of the squares of the other two sides:
x2 + y2 = 12
But 12 is just 1, so:
x2 + y2 = 1
(the equation of the unit circle)
Also, since x=cos and y=sin, we get:(the equation of the unit circle)
(cos(θ))2 + (sin(θ))2 = 1
a useful "identity"
Important Angles: 30°, 45° and 60°
You should try to remember sin, cos and tan for the angles 30°, 45° and 60°.Yes, yes, it is a pain to have to remember things, but it will make life easier when you know them, not just in exams, but other times when you need to do quick estimates, etc.
These are the values you should remember!
| Angle | Sin | Cos | Tan=Sin/Cos |
|---|---|---|---|
| 30° | 1 √3 = √3 3 | ||
| 45° | 1 | ||
| 60° | √3 |
How To Remember?

sin(30°) = √12 = 12 (because √1 = 1)
sin(45°) = √22
sin(60°) = √32
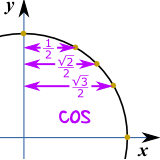
And cos goes "3,2,1"
cos(30°) = √32
cos(45°) = √22
cos(60°) = √12 = 12
Just 3 Numbers
In fact, knowing 3 numbers is enough: 12 , √22 and √32Because they work for both cos and sin:
 |
Comments
Post a Comment